Zeigen Sie z.B. mithilfe der 1. Ableitung, dass die Funktion nur eine NS hat.

Question

wie kann man zeigen, dass die Funktion:

f(x) = 1,25x³ +1,25x -0,26 

nur eine Nullstelle hat?

Answer 1

Hallo Alpi,

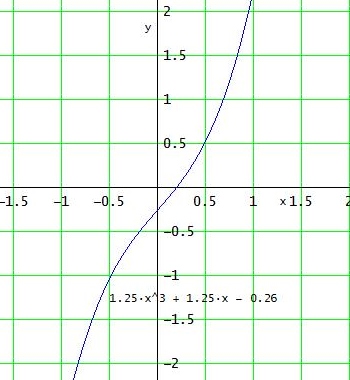
f(x) = 1,25x³ + 1,25x -0,26 

f '(x) = 3,75 x² + 1,25  > 0  für alle x∈ℝ

Da die Steigung überall positiv ist, ist die Funktion streng monoton steigend.

Sie kann also höchstens eine Nullstelle haben.

Wegen  lim_x→∞ f(x) = ∞  und   lim_{x→ -∞}   f(x) =  - ∞   hat sie nach dem Zwischenwersatz mindestens eine Nullstelle. 

[ Letzteres  ist bei jeder Polynomfunktion mit D=ℝ so, deren höchste x-Potenz einen ungeraden Exponenten hat. ]

Also hat sie genau eine Nullstelle.

Gruß Wolfgang

Comments

Hallo Wolfgang, nachträglich noch eine kurze Frage, vielleicht auch eine etwas blöde. Die erste Ableitung ist überall positiv, wenn alle Werte postiv sind. Also wäre f'(x) = x² - x + 1 =0  nicht streng monoton steigend oder? Ein kurzes richtig reicht mir schon.  

---

eine solche nach oben geöffnete Parabel ist

- streng monoton fallend von -∞ bis zur Scheitelstelle und

-  streng monoton steigend  von der Scheitelstelle bis ∞

also nicht streng monoton

Answer 2

Die Lösung von Wolfgang ist natürlich richtig. Eine recht aufwändige Alternative wäre: Teile die Gleichung durch 1,25. Dem Ergebnis x³+x-0,208 = 0 sieht man die Lösung x=0,2 gut an. Eine Polynomdivision durch (x-0,2) führt zu einer quadratischen Gleichung, die keine reelle Lösung hat.