Reihe 1/n^2 sowohl konvergent als auch divergent?

Question

wenn die Reihe bei n=0 anfängt sagt wolfram alpha, es existiert keine summe aufgrund einer singularität..

Heisst mit anderen Worten wenn ich bei = 0 anfange dann divergiert die Reihe=?

wenn die reihe hingegen bei n=1 anfängt konvergiert sie gegen Pi^2/6

Was i´ch mich jetzt frage ....Warum ist das so?

wenn ich bei n=0 anfange kommt der Summe doch lediglich 1 hinzu...

weil 1/1^0 = 1.

Answer 1

Hi,

Division durch 0 ist nicht erlaubt. Für n=0 ist die Summe gar nicht definiert.

Answer 2

1^0 =1 stimmt zwar. Aber du sollst rechnen:

0^2 = 0*0 = 0

1/0^2 = 1/0 ist eine verbotene Operation.

Answer 3

   " Null hoch ein negativer Exponent " gibt immer Unendlich. Vielleicht ist Analysis doch ganz vernünftig; dieser Reihenzirkus setzt natürlich voraus, dass die einzelnen Terme deiner Reihe auch wohl definiert sind. Wir hatten Walter Keim, einen höchst bissigen assistenten

   " Em Erstsemester derfste nix glaube. Die könne noch nettemaa denke. Unn des Schlimmste; die meine, 's weer wüükisch so, wiese saache. Nachher im 7. Semester kannse schon emaa Pippifax mache; des wüüd dann schon net missverstanne.  "

   Und dann sagte er noch

   " Die ganze Genosse wolle als net kapiern, dass das Verhalten einer Folge bzw. Reihe IM ENDLICHEN nix über ihre Konvergenz aussaht. "

    wenn du ein glied weg lässt - intressiert doch keinen.

   Warum konvergiert deine Reihe? Schau mal hier, was Pappi alles weiß

https://de.wikipedia.org/wiki/Integralkriterium

    Wetten, dass das nicht dran war in der Vorlesung?

Answer 4

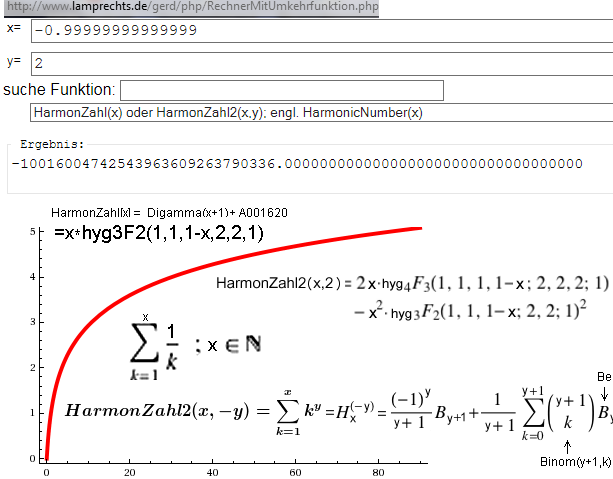
§1: für n=0 ergibt sich 1/0² und nicht 1/1^0

damit ist es eine Polstelle die gegen Unendlich divergiert (eigentlich nicht definiert ist)

§2: schon bei Deiner letzten Frage habe ich versucht Dir zu zeigen, dass die explizite Funktion zu dieser Summe viel universeller als der Summen-Algorithmus ist, da er nur mit ganzzahligen Argumenten funktioniert.

Also einsetzen ergibt:

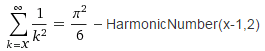
Diese Funktion rechts des Gleichheitszeichens ist für reelle Argumente gültig und ergibt geplottet:

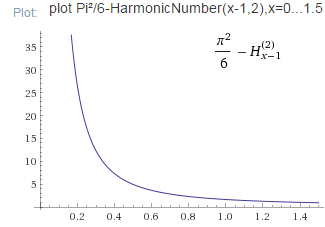
Auch hier erkennt man die Divergenz gegen Unendlich, wenn x gegen 0 geht,

weil HarmonZahl2(x,2) bei x gegen -1 im Funktionswert gegen -Unendlich divegiert.

Hinweis: HarmonZahl2(x,1)=HarmonicNumber(x)  {wenn y=1 kann man 2. Argument weglassen}

Funktionswerte und Berechnungsalgorithmus per hypergeometrischer Funktion hier:

http://www.lamprechts.de/gerd/php/RechnerMitUmkehrfunktion.php

Comments

HallO hyperg

Danke für deine ausführliche Antwort.

Leider bin ich noch unerfahren auf diesem gebiet..

Und deine Antwort sah etwas komplizierter aus...

Da muss ich mir mal etwas mehr Zeit nehmen.

Meine Frage hier ist absoluter Schwachs..n ..Ich habe nur gepennt bei dieser überlegung.

Natürlich darf nicht durch null geteilt werden.