Vektoren Problemstellung in Aufgabe zwei mit Vektoren von Aufgabe 1 lösen? Oder wie?

Question

Hallo leutz,

Ich habe bei folgender Aufgabe einige Verständniss-Fragen.

Undzwar weiss ich nicht was mit der Aufgabe 2 gemeint ist.

Muss ich hier die Vektoren der vorherigen Aufgabe verwenden und einen Ansatz über eine Lösung würde ich mich freuen da ich nicht weiss wie man sowas allgemein löst.

Danke für eure Mühe :)
 

Answer 1

  Ist dir eigentlich klar, dass v1 und v2 aufeinander senkrecht stehen? Bei meiner Routine mit drei Silvestern Mensa sieht man das; d.h. das Skalarprodukt < v1 ; v2 > ist immer Null ( Ich hab voor gee-saagt !!! ) Das Kreuzprodukt ist dann dem Betrage nach gleich der Rechteckfläche.

   Bloß was " c " sein soll. Das haben wir noch nicht gehabt ... Muss wohl auf einem Zettel stehen, den du uns aus Versehen nicht gezeigt hast.

Comments

c wird in Teil 1a) definiert.

Answer 2

Schau mal dort,

https://de.wikipedia.org/wiki/Kreuzprodukt#Komponentenweise_Berechnung

also für Teil b :

4

-8

4

Comments

Und wie zeichne ist das ?

Aufgabe 1 ist eher das kleinere Problem aber bei Aufgabe 2 blicke ich gar nicht durch.

---

https://www.matheretter.de/geoservant/de?draw=vektor(0%7C0%7C0%203%7C2%7C1)%0Avektor(0%7C0%7C0%201%7C2%7C3)%0Avektor(0%7C0%7C0%204%7C-8%7C4)

---

Und für Teil 2 etwa so:

< v1 ; v2 > = r^2 * ( cos(φ)* -sin(φ)  +  sin(φ)*cos(φ) ) = r^2 * 0 = 0

also stehen v1 und v2 aufeinander senkrecht.

v1 x v2 = ( ...   Komponenten ausrechnen und dann kommt bei

v3 * e3 wohl  r^2 raus, also der FI des von v1 und v2 aufgespannten Quadrates.

Answer 3

Aufgabe 2 hat nichts mit den Zahlen aus Aufgabe 1 zu tun.

Beginne mit v1. "Die Ellipse" ist ein Kreis mit Radius r in der Grundebene. phi habe ich so gewählt, dass v1 ein Vektor im 1. Quadranten ist. Also (0°< phi < 90° ).  

 

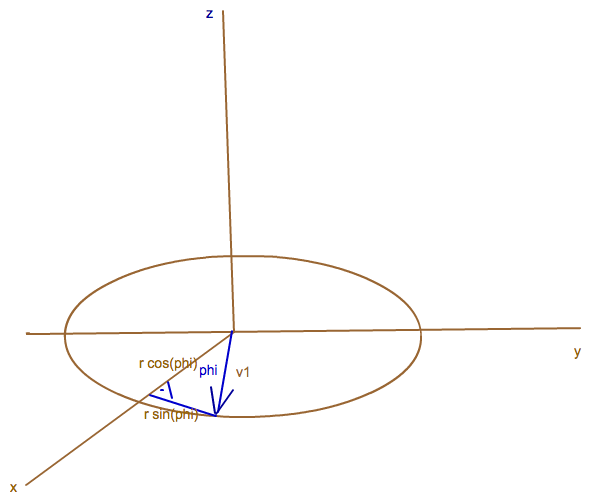
Damit kannst du dann auch v2 einzeichnen (liegt ebenfalls in der Grundebene und steht senkrecht auf v1) .

Ich nehme an, dass das im Graphen von mathef alles angezeigt wird. - (Klappt mit meinem Bildschirm leider nicht. EDIT: Nein mathef hat Aufgabe 1 illustriert)

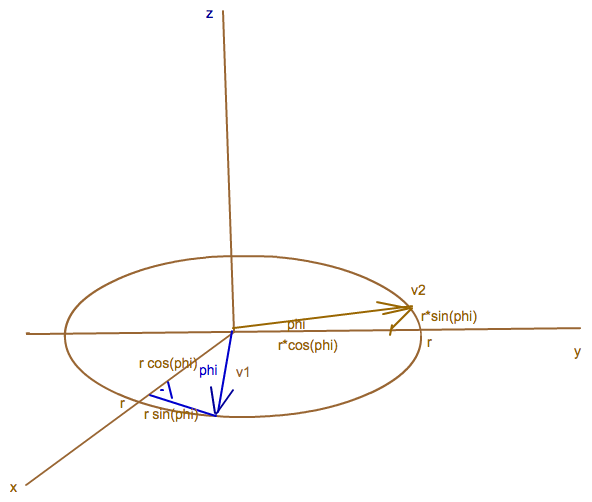
und nun die Eigenschaften und weitere Details

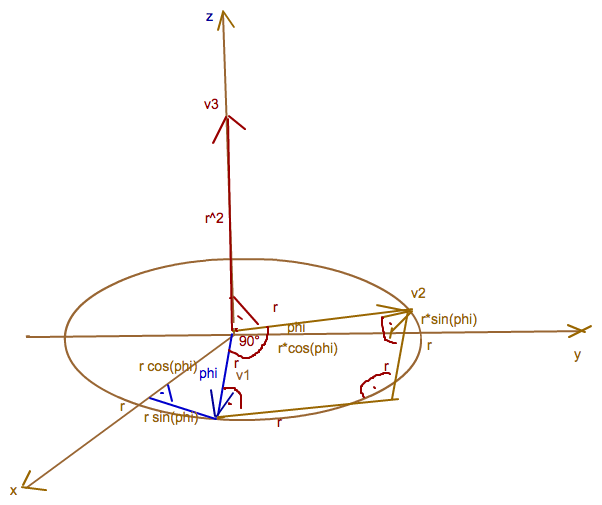
Die Produkte berechnest du dann direkt mit den Buchstaben phi und r (ohne Zahlen einzusetzen). 

Beim Skalarprodukt sollte 0 rauskommen, da die Vektoren senkrecht aufeinander stehen. Beim Vektorprodukt r^2, da die beiden Vektoren ein Quadrat mit Seitenlänge r aufspannen. 

e_(3) ist übrigens der Vektor (0,0,1)^tr

v_(3) = (0,0,r^2) 

v_(3) * e_(3) = r^2. 

Comments

Danke für deine Hilfe und Mühe Lu.

Ich habe da direkt mal ein paar Fragen wenn ich den Vektor v1 in den Plotter von Geoknecht einsetze, was muss ich dann eingeben. Also wie heisst der Befehl.

Ich habe da einige Verständnis schwierigkeiten, undzwar sieht der Vektor v1 und v2 für mich gar nicht so aus wie ein Vektor, da dort einmal sin und cos drin sind und dann noch ein r vor dem ganzen gesetzt ist. Vieleicht könntest du mir das mal genauer erklären.

Danke für deine Hilfe :)

---

Tipp: Versuche so oft wie möglich das Neue mit dem zu verbinden, das du bereits weisst. So lernt es sich einfacher und du behältst den Überblick. 

phi ist ein griechischer Buchstabe. Diese werden für Winkel benutzt.

Der beiden gleichen Winkel phi in meinen Bildern liegen in der Grundebene. 

Hier erfährst du, wie man sinus und cosinus am Einheitskreis abliest:

https://www.matheretter.de/wiki/einheitskreis

Rubrik: "Wie kann man Sinus- und Kosinuswerte am Einheitskreis ablesen? "

Weil die Vektoren die Länge r und nicht 1 haben, ist bei dir in der Grundebene alles um den Faktor r gestreckt. Deshalb hast du rechtwinklige Dreiecke, in denen du die Katheten mit r*sin(phi) und r*cos(phi) anschreiben kannst.

Wenn du das erste Video im Link verstanden hast, kannst du dir dort die Drehung um 90° problemlos vorstellen und dann das Gelernte in die Grundebene des oben skizzierten 3D-Koordinatensystems übertragen. 

---

Der Einheitskreis ist für mich geläufig, wusste das so gesehen schon, nur eben halt nicht in Form einer Ebene, als Vektorschreibweise und gerade das wird in dem Link auf den du dich beziehst nicht angegeben. Geometrische Formen mit einem Vektor zu repräsentieren ist mir halt neu und deswegen verstehe ich diese Schreibweise nicht und da liegt auch schon meine Frage versteckt wie siehst du aus einem Vektor mit sinus und kosinus eine Ebene, die eine Kreisscheibe ist.
Das verstehe ich nicht.

---

Das ganze ist ja sogar transponiert

---

Wenn ich das transponiere dann hätte ich doch r *sin(phi), r * cos(phi) und r* 0 oder etwa nicht ?

---

"Das ganze ist ja sogar transponiert "

Transponiert heisst nur, dass du die Komponenten untereinander schreiben sollst, wie man das normalerweise bei Vektoren macht, um sie graphisch von Punkten zu unterscheiden. 

---

Habs ja hingeschrieben wie es transponiert sein könnte.

---

"Wenn ich das transponiere dann hätte ich doch r *sin(phi), r * cos(phi) und r* 0 oder etwa nicht ? "

Du hast untereinander

(  r *sin(phi), 

  r * cos(phi) 

     r* 0                  )

=

(  r *sin(phi), 

  r * cos(phi) 

     0                  )

---

Ja das was du untereinander geschrieben hast habe ich in einer Zeile geschrieben um Platz zu sparen. ^^

---

Oder muss ich das explizit untereinander schreiben ?

---

Das ist beides gleichwertig:

entweder du schreibst die Komponenten untereinader

oder du schreibst sie nebeneinander und dann ^T dahinter-

---

Ok und wie komme ich darauf das es eine Kreisscheibe ist, also eine Ebene die ein Kreis auf der Grundebene ist ?

Ich habe da bereits eine Vermutung, da r*0 = 0 ist, ist z = 0 und somit liegt die Ebene auf der Z Achse nach oben hin an der Stelle 0 und somit am Koordinatenursprung ?! Wie komme ich jetzt aber darauf das es ein Kreis ist ?

---

also wenn r * cos(phi) mit phi E (-pi|pi) wäre dann hätte ich auf der x Achse einmal -1 und 1. Bei r*sin(phi) mit phi E (-1|1) hätte ich dann -1 und 1 auf der Y Achse.

---

Also wenn ich dann noch den Radius mit r = 1 setze dann wäre das ein Kreis mit einem Radius 1 der die Achsen bei x = 1,  x = -1 und bei y = 1, y = -1 schneidet ? Wäre das die Erklärung ?

---

Wenn du r= 1 und bei v1Folgendes wählst: x=1, ist automatisch phi = 0 und y = 0. Du hast dann nur einen Spezialfall skizziert. Das darfst du auch. Bestimme den zugehörigen Vektor v2. 

Dann skizzierst du noch ein paar weitere Fälle (mit andern Winkeln) und wirst zum Schluss kommen, dass immer um 90° gedreht wird. 

Meine Skizzen oben waren gleich etwas allgemeiner. 

Ich habe jetzt einen meiner ersten Sätze etwas geändert und hoffe er ist nun verständlicher:

" Beginne mit v1. "Die Ellipse" ist ein Kreis mit Radius r in der Grundebene. phi habe ich so gewählt, dass v1 ein Vektor im 1. Quadranten ist. Also (0°< phi < 90° ).  " 

---

Deine Erklärung haut mich wieder komplett raus. Warum: Was soll ich bei v1 wählen x = 1 kann ich da doch gar nicht einsetzen, wenn phi ein Bogenmass ist

---

und phi ist nicht von 0 bis 90 Grad sondern von -180 bis 180 Grad

---

Wie kommst du darauf das phi von 0 bis 90 Grad sein kann ?

---

phi kann gemäss Aufgabe von -180° bis + 180° gehen.

Meine Skizzen ist für den Fall phi zwischen 0° und 90° gemacht. Liegt v1 in einem der anderen Quadranten musst du im Prinzip nochmals weitere Skizzen machen, wenn du die Drehung um 90° noch nicht erkannt hast. 

---

Wie hast du v1 exakt bestimmt  ? zwischen 0 und 90 Grad könnte der Pfeil ja auch einfach bei 45 Grad liegen oder?

---

Ja. Kann man.  Aber für Skizzen, die "allgemein" sein sollen, ist es gescheiter einen Winkel zu wählen, bei dem keine spezielle Symmetrie die Schlussfolgerungen verfälschen sollte. 

---

Hi, wenn du für phi einen Wert einsetzt, erhältst du einen Punkt in der Ebene. Da aber viele versch. Werte für phi einsetzen kannst, erhältst die eine Kurve, die hier ein Kreis darstellt. 

---

Wie heisst denn das Stichwort zu diesen Matrizen. Dann kann ich mir das mal anschauen.

---

Oder so warum ist bei x = 1; phi = 0

---

weil x=r*cos(φ)

--> x=r*cos(0)=r*1=r=1 (wenn man den Einheitskreis betrachtet)

---

Damit hast du aber nicht gesagt das aus der Rechnung x = 1 hervorgeht sondern sagst wenn phi = 0 ist dann auch x = 1 ist wegen dem cosinus. Der Radius ist damit dann aber noch nicht 1

---

Also aus der Rechnung ist der Radius nicht 1 sonder r*1 aber mit dem Einheitskreis ist der Radius ja auf eins gesetzt.

---

Ja richtig. Ich hatte verstanden, dass du für deine Beispiel r=1 genommen hast. (Das ist eine gute Idee). Finde nun aber die Stelle nicht mehr und zitiere nur mal: "Warum: Was soll ich bei v1 wählen x = 1 kann ich da doch gar nicht einsetzen, wenn phi ein Bogenmass ist  ". Man kann sowohl r als auch phi selber wählen. Aber für die Beispiele / Skizzen muss man sich mal für irgendwas entscheiden. 

---

Wie groß ist der Winkel zwischen Vektor v1 und der x Achse ?

---

Der misst phi. Du kannst für phi wählen, was du willst. 

Hier meine Wahl in der Skizze oben: (Habe einen Winkelbogen ergänzt). 

Von oben siehst du phi so wie in der Abbildung von jc2144 oder wie das Alpha im Video, das ich in meiner Antwort verlinkt hatte. 

Ab nun ist in der Skizze phi und r bestimmt. 

Nächste Skizze etwas genauer angeschrieben:

Ich habe bei v2 auch schon einen Bogen bei phi eingezeichnet und den rechten Winkel mit /. versehen. 

r*cos(phi) ist in y-Richtung perspektivisch weniger stark verkürzt wie in y-Richtung. (Analog bei r*sin(phi) )

Du kannst dir aber auch eine Ansicht von oben zeichnen, damit du die rechten Winkel besser erkennen kannst. Lasse dich auch hier vom verlinkten Video inspirieren. 

---

Also für mich ist da jetzt kein Unterschied zu den anderen Skizzen :D
Habs schon angesehen und wie bereits gesagt als Ebene sowas zu Zeichnen in einem 3 dimensionalen Raum ist nochmal eine Ecke anders. Vom Winkel Phi hast du eigentlich nichts verändert, der selbe Winkel. Ich könnte es wenn sowas in einer Klausur auftreten würde nicht Zeichnen.

---

Ich komme auf die selbe Lösung aber habe auch alles selber nachgerechnet aber das zeichnen kriege ich nicht hin

---

Du kannst an einer Klausur phi wählen, wie du willst. - Oder direkt eine Ansicht von oben zeichnen (mit frei gewähltem phi).

Ich gehe davon aus, dass du an der Klausur einfach wissen musst, dass alles mit r*sin(phi) und r*cos(phi) irgendwie auf eine Drehung um 90° oder eine Spiegelung herausläuft. Da hast du keine Zeit so lange zu zeichnen, bis du weisst, was geschieht. 

---

Genau so ist das.

---

Bei einer mündlichen Prüfung ist das einfacher: Da kannst du es 3-dim. erklären z.B. indem du die Tür  oder ein Fenster öffnest. Wenn das nicht möglich ist, geht es auch mit einem Buch, das du aufstellst und unterschiedlich stark öffnest. 

---

Ich versuche es nochmal.
Wenn ich v1 zeichnen möchte, dann weiss ich das mit der komponentenschreibweise

( r*cos(phi)

r*sin(phi)

r*0

)

Laut dem Text in der Aufgabe soll ich ein bel. aber fest vorgegebenes r zwischen 0 und unendlich wählen. Zudem soll ich auch ein bel aber fest gewähltes phi zwischen -phi und phi auswählen. Also könnte ich auch sagen mein phi ist zwischen 0 bis 90 grad Hauptsache es ist zwischen -180 und 180 Grad.

Ich wähle für x = r * cos(phi = 0) Dann erhalte ich für phi = 0; x = 1. In x Richtung müsste dann v1 zuerst in x Achsen Richtung um eins nach vorne vom Ursprung aus zeigen da z = 0 ist. Anschliessend das selbe für y = r*sin(phi ist 0) also ist in y Achsen Richtung Null und der Pfeil muss genau Senkrecht nach unten unterhalb der z Achse den Kreis berühren aber nicht schneiden. Das selbe für v2 und dann habe ich v1 und v2 gezeichnet. v3 habe schon anhand deiner Skizze verstanden. Ist das denn soweit korrekt ?

---

Nein sorry der Pfeil geht vom Ursprung zu x = 1, da der Vektor nun (1,0,0) lautet

---

v2 wäre hätte dann die Koordinaten (0,1,0) und der Pfeil würde dann vom Ursprung aus nach y bei y = 1 zeigen.

---

Gut. Du hast in den letzten beiden Kommentaren ein Beispiel richtig beschrieben.

Beispiel r = 1 und phi = 0.

" Pfeil von v₁ geht vom Ursprung zu x = 1, da der Vektor nun v₁ = (1,0,0)^tr lautet . 

v₂ wäre dann v₂ = (0,1,0)^tr und der Pfeil würde dann vom Ursprung aus nach y bei y = 1 zeigen. "

Setze über die fett geschriebenen Buchstaben noch einen Vektorpfeil und ergänze ^tr für transponiert (wie in der Fragestellung) oder schreibe die Vektorkomponenten untereinander auf dein Blatt. 

---

Du hast daraus direkt mit r^2 die Vektorpfeile zu einem Quadrat ergänzt.
Warum kann ich das mit r^2 machen. Ich weiss, dass r^2 eine Fläche eines Quadrates ist aber das ist doch noch kein Quadrat.

---

https://de.wikipedia.org/wiki/Kreuzprodukt

Ein (aufgespanntes) Parallelogramm mit einem rechten Winkel, der zwei gleich lange Schenkel hat, ist automatisch ein Quadrat. 

Im gleichen Link findest du auch die Formel, mit der du v₃ = v₁ x v₂ zu berechnen hast. 

Selbstverständlich sollten solche Formeln auch in deinem Theorieheft /-buch stehen, bevor man dich auf solche Aufgaben loslässt.

Diese Aufgabe könnte dich nun z.B. in Zylinderkoordinaten einführen. Vgl. https://de.wikipedia.org/wiki/Polarkoordinaten#Zylinderkoordinaten

Formeln im obigen Link (wenn nicht in eurem Heft).