Potenzrechnung mit Ausklammern,

Question

,

Demnächst fängt mein IT Studium an und zur Zeit schaue ich mir den dazugehören Vorkurs für Mathematik an.

Soweit komm ich eigentlich ganz gut zu recht, jedoch hänge ich bei einer Aufgabe wo ich mir die Herleitung  des Ergebnis nicht erklären kann.

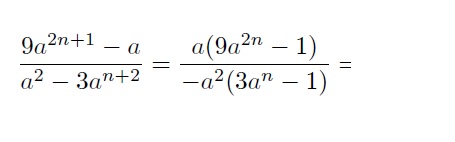
Ich versteh bei der Aufgabe nicht wie man bei den Nenner auf die -a^{2}(3a^{n}-1) kommt.

Wenn ich denn Nenner zurück rechne bekomme ich -3a^{n+2} + a^{2} raus, was ja auch irgendwie logisch ist.

Nur wenn ich an die Aufgabe rangehen würde, hätte ich auch nur a^{2} ausgeklammert und wäre zum Ergebnis  a^{2}(1-3a^{n}) gekommen.

Mir scheint es hier, als wäre der Nenner einfach mal *-1 gerechnet worden. Versteh ich das richtig?

Ich bin wirklich ratlos, und wäre über eine Aufklärung sehr dankbar :)

Comments

Vielen Danke für die schnellen Antworten...ich war einfach so fixiert auf dieses Ergebnis ,richtige Denkblockade gehabt,

Answer 1

Hi,

es wurde nur erkannt, dass es von Vorteil ist ein positives Vorzeichen vor 3a^n zu haben. Deswegen wurde statt a^2 eben -a^2 ausgeklammert. Wäre aber beides richtig. Du würdest in einem späteren Schritt -1 ausklammern müssen :).

Grüße

Answer 2

Nenner:

a²(1-3aⁿ) 

kannst du schon so machen.

Dann musst du einfach im Zähler bei 9a^2 - 1 den versteckten 3. Binom erkennen und dann später noch irgendwo ein Minus ausklammern. 

9a^2n - 1 = (3a^n - 1) ( 3a^n + 1) = - (1-3a^n)(3a^n + 1) 

Answer 3

a^2 -3 a^{n+2}

Anwendung Potenzgesetze:

allg: a^n *a^m=a^{m+n}

=a^2 -3a^n *a^2

=-a^2(-1 +3 a^n)