Bestimmung der Extremwerte der Höhen des Betonteilers.

Question

Hallo , brauche ein bisschen hilfe bei der Aufgabe :

Zur Verschalung eines 6m langen Betonfertigteiles ist die obere und untere Berandung des Querschnitts durch die Funktion f und g mit:         

f(x)=( -1/10)*x^{3} + (9/10)*x^{2} -( 9/5)*x +3      bzw.   

 g(x)= (-1/4x)*x^{2} + (3/2)*x       

festgelegt (Maße in m). Bestimmen Sie die Stellen, an denen die Höhe h des Betonteiles am größten bzw. am kleinsten ist. Wie hoch ist an diesen Stellen das Betonteil jeweils?

Bild: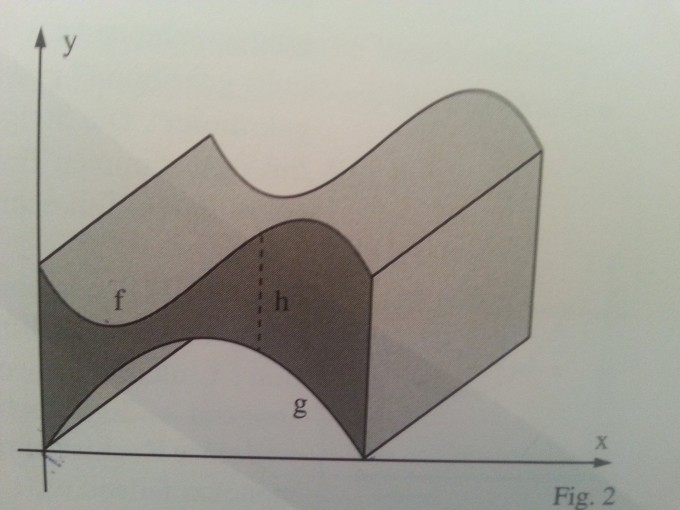 

Noch eine Bitte Ich brauche eine vollständige Lösung der Aufgabe damit ich verstehe wie man diese Aufgabe berechnen kann . Vielen Dank für eure Mühe .

Answer 1

f(x) = - x^3/10 + 9·x^2/10 - 9·x/5 + 3

g(x) = 3·x/2 - x^2/4

h(x) = f(x) - g(x) = - x^3/10 + 23·x^2/20 - 33·x/10 + 3

h'(x) = - 3·x^2/10 + 23·x/10 - 33/10 = 0 --> x = 5.755 ∨ x = 1.911

h(1.911) = 0.1955 --> TP

h(5.755) = 3.036 --> HP

Comments

Man sollte wissen das rein rechnerisch die Höhe bei x = 7.735 ca. 0 ist. Aber das ist sicher nicht mehr im Definitionsbereich. Zumindest ist der Bereich nicht mehr in der Skizze zu sehen.

---

Ja, x = 7.735 ist sicher nicht im hier zu unterstellenden Definitionsbereich [0;6]. Zur Rechnung gehört aber auch noch die Betrachtung der beiden Ränder!