Aufgabe Pyramidenzelt:
Ein Zelt hat die Form einer geraden quadratischen Pyramide mit 8 m Breite und 3 m Höhe. Den Eingang bildet das Trapez EFGH mit |EF| = 4 m und G bzw. H als Mitten der Strecken \( \overline{ES}\) bzw. \( \overline{FS}\).
a) Wie groß ist der Eingang EFGH?
b) Ein Meter unter der Zeltspitze S befindet sich eine Lichtquelle. Durch den Eingang fällt Licht nach außen und der Schatten der Zeltwand begrenzt so eine beleuchtete Fläche. Wie groß ist sie?
c) Wie ändert sich die beleuchtete Fläche, wenn die Lichtquelle weiter nach oben bzw. weiter nach unten gebracht wird?
Welche Grenzflächen ergeben sich, wenn sich die Lichtquelle in S bzw. in 1,5 m Höhe befindet?
d) In der Mitte der hinteren Zeltkante \( \overline{CD} \) ist auf einer senkrechten Stange eine Kamera angebracht. In welcher Höhe muss sie sich befinden, wenn sie die gesamte beleuchtete Fläche überwachen soll?
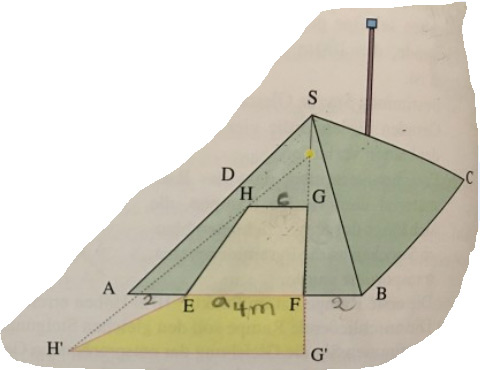
Wie löst man Aufgabe a? Bitte nicht nur die Lösung das bringt nicht zum selber lernen und verstehen.