f(x)=4*sin(0,5(x-7,4))=3 nach x auflösen

Question

Ich versuche es schon seit Stunden, aber meine Ergebnisse passen nicht zum Graphen.

Wie rechne ich f(x)=3 von der Funktion f(x)=4*sin(0,5(x-7,4)) ?

(Bitte mit Rechnung, damit ich meinen Fehler finden kann)

Answer 1

4*sin(0,5(x-7,4)) = 3

sin(0,5(x-7,4)) = 3/4

mit k∈ℤ:

0,5(x-7,4) = arcsin(3/4) + k·2π   oder  0,5(x-7,4) = π - arcsin(3/4)  + k·2π         | • 2

  x - 7,4 = 2 • arcsin(3/4) + k·4π  oder x -7,4 = 2π - 2• arcsin(3/4) + k·4π   | + 7,4

x = 2•arcsin(3/4) + 7,4  + k·4π  ≈ 9.096 + k·4π  

oder   x = 2π - 2• arcsin(3/4) + 7,4 + k·4π ≈ 11.987

z.B.

Für k = 0   →   x₀₁ ≈ 9.096   ;    x₀₂ ≈ 11.987

für k = -1    →   x_-11 ≈ - 3,47   ;    x_-12 ≈  -0.579

---

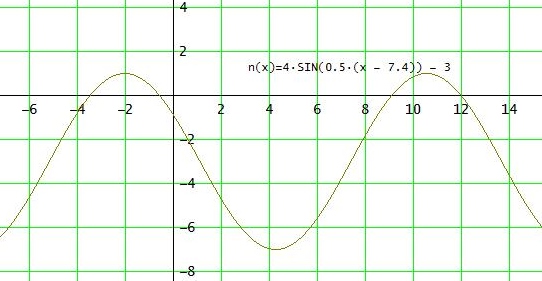
Für die Funktion n(x) = 4·SIN(0.5·(x - 7.4)) - 3 erscheinen die Lösungen als Nullstellen:

Gruß Wolfgang