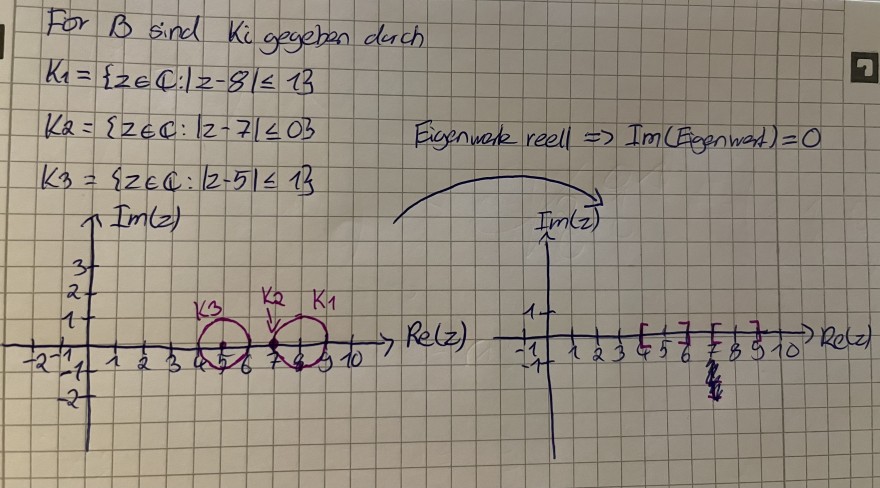
Betrachten wir nun zu eine Matrix A (mit i Zeilen und j Spalten) die zugehörigen Gerschgorin Kreis Ki
Ki ={z∈ℂ: |z-aii| ≤ ri } mit ri = ∑j=1,i≠j (aij).
Wir betrachten also Kreise in der komplexen Zahlenebene. ( x-Achse = "Realteil von z", y-Achse = "Imaginärteil von z").
Die Gerschgorin Kreise geben also Gebieten an in denen die Eigenwerte von A liegen.
Naja und zusätzliche wissen wir, dass Matrizen, welche symmetrisch und reell sind, immer reelle Eigenwerte haben. Somit ist der Imaginärteil dieser Eigenwerte gleich 0.
Wenn wir jetzt unsere reellen Eigenwerte in der komplexen Zahlenebene anschauen, so macht es nur Sinn, Intervalle anstatt Kreise für die Gebiete unserer Eigenwerte zu betrachten. Da die Eigenwerte sowieso keine Werte außerhalb der reellen Zahlengerade annehmen können.