Fixpunkte, Lineare und Quadratischen Funktionen berechnen?

Question

!

Ich habe bei einigen Mathe Aufgaben Schwierigkeiten und hoffe ihr könnt mir helfen. Ich weiß einfach nicht wie ich auf die Lösungen komme. Ich sitze schon eine gefühlte Ewigkeit daran und mir fällt einfach nichts ein!

Aufgabe 1) Der Graph einer linearen Funktion verlaufe durch die Punkte P(0|1) und Q(a|f(a)) mit a ≠ 0. Geben Sie die Funktionsgleichung der Funktion an.

Aufgabe 2) Betrachten Sie die Gaußsche Summenformel ∑ⁿ_{i = 1} i = n(n+1)/2 als Funktion G: ℕ → ℕ, n ↦ n(n+1)/2.

a) Geben Sie den Grad der Funktion an.
b) Berechnen Sie die Fixpunkte der Funktion.

Aufgabe 3) Die Abbildung (siehe Bild) zeigt den Graph von f(x) = x² + 1. Sei P(a|f(a)) ein Punkt auf der Parabel mit a ≠ 0. Was gilt für die Steigung m einer Geraden durch P und den Ursprung?

Angaben zum Bild:

(a) m = a²1/ a   (b) m = 2a   (c) m = f(x)   (d) m = 0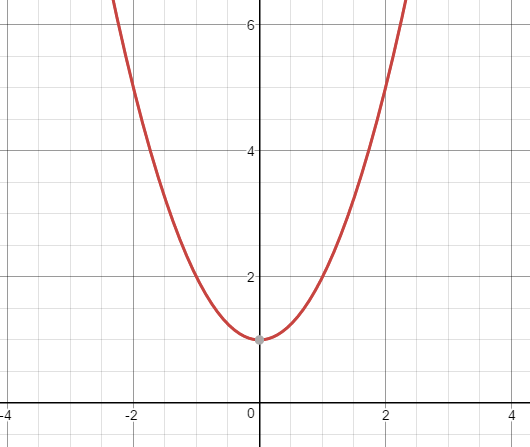

Ich weiß ehrlich gesagt zum Teil gar nicht was Verlangt wird, da ich die Aufgabenstellung an sich nicht verstehe. Alle anderen habe ich zumindest ansatzweise gelöst. Nur bei diesen drei bin ich am verzweifeln!

Comments

Ich komme bei einer Aufgabe nicht weiter...

Der Graph einer linearen Funktion verlaufe durch die Punkte P(0|1) und Q(a|f(a)) mit a ≠ 0.

Aufgabe: Geben Sie die Funktionsgleichung der Funktion an.

---

Habe ich soeben beantwortet. Die Frage wurde schon gestellt.

---

Warum "antwortest" du dann noch einmal? Für so etwas gibt es Kommentare.

---

Erst einmal vielen Dank für die Antwort! Wie genau sind Sie auf die Lösungen gekommen? Eine kurzer "Weg" zu den Lösungen wäre nett, damit ich das auch nachvollziehen und verstehen kann. =)

---

Zu 1) Auf der Geraden gibt es einen konkreten Punkt (0/1) und zwei allgemein formulierte Punkte (a/f(a)) und (x/y). Dann lässt sich die Steigung der Geraden einmal so (f(a)-1)/(a-0) und einmal so (y-1)/(x-0) ausdrücken. Bei Geraden ist die Steigung überall gleich (f(a)-1)/(a-0) = (y-1)/(x-0).

Zu 2 a) Wie man den Grad einer Funktion herausfindet, weißt du sicher selbst.

Zu 2b) Hier hatte ich meine Antwort mit "Wenn...." begonnen. War diese Annahme zutreffend?

Zu 3) Zwischen den Punkten (0/0) und (a/a²+1) liegt die Steigung (a²+1 - 0)/(a - 0).

---

Guten Tag allerseits!

Ich habe hier vor kurzem eine Frage gestellt und diese wurde auch beantwortet. Die Aufgaben wurden mir auch zum Teil erklärt aber dennoch habe ich es nicht verstanden.

Die Aufgaben: https://www.mathelounge.de/376908/fixpunkte-lineare-und-quadratischen-funktionen-berechnen

Was ich nicht verstehe bzw. wo ich den Überblick verliere ist z.B. bei der ersten Aufgabe, wo vieles in klammern steht. Mein größtes Problem: Ich kann mir nicht nicht vorstellen, wie das zeichnerisch aussehen würde. Was ist der erste Schritt und wie komme ich von selbst darauf, wie ich anfangen muss? Auch bei Aufgabe 2 weiß ich ernsthaft nicht, wie ich den Grad der Funktion erkennen kann. Anfangs hätte ich gesagt, die Funktion hat den Grad eins, da kein ^2 vorhanden ist. Wie berechne ich genau die Fixpunkte? Auch bei Aufgabe 3 wie muss ich vorgehen und wie würde es zeichnerisch aussehen?

Ich bräuchte eine Erklärung für "nicht Mathe Menschen". Einfach nachzuvollziehen und übersichtlich.

Ich weiß, das ist eine Menge und viel Aufwand aber ich möchte das alles verstehen und es lernen. Ich möchte eine gute Arbeit schreiben und während der Klausur, kann ich nicht mal eben hier etwas fragen. Ich wäre euch sehr dankbar! 

---

Nachfragen zu Aufgaben solltest du immer bei der konkreten Aufgabe stellen.

Meist langt hier für die Antwortenden nicht die Zeit aus die ganzen Grundlagen, die hinter Aufgaben stecken zu wiederholen. Daher ist es günstig, wenn du in der Antwort genau erklärst was du nicht verstehst.

Wenn du viele Probleme bei Grundlagen hast, kann es sinnvoll sein sich ein Mathebuch zu besorgen in dem Genau diese Grundlagen aufgearbeitet werden oder du fragst bei https://www.mathelounge.de/tutors/ um Rat.

Im privaten Einzelgespräch kann man natürlich viel besser und gezielter auf deine Probleme eingehen.

Answer 1

Zu 1) (f(a)-1)/a=(y-1)/x oder y = (f(a)-1)x/a+1.

Zu 2a) Die Funktion hat den Grad 2.

Zu 2b) Wenn ein Fixpunkt entsteht, weil x = f(x) ist, dann ist (1/1) ein Fixpunkt.

Zu 3) P(a/a²+1) Steigung der Geraden OP (a²+1)/a.

Answer 2

Ich hatte ja versucht, deine Fragen zu beantworten. Den Grad einer Funktion erkennt man am höchsten Exponenten des Funktionsterms. Ich hatte da eine 2 gesehen. Wenn ich mich geirrt habe, tut es mir leid. Meine Frage, was denn normalerweise "Fixpunkt" genannt wird, hast du auch nicht beantworten können. Dann kann ich dir hier nicht helfen