1. Geradengleichungen aufstellen
Gerade AB: (x|y|z) = (-7|-3|-8) + r1·(5|3|-1)
Gerade CD: (x|y|z) = (4|-6|-6) + r2·(3|5|-2)
Dann Schnittpunkt S berechnen:
2. Geradengleichungen gleichsetzen
AB = CD
(-7|-3|-8) + r1·(5|3|-1) = (4|-6|-6) + r2·(3|5|-2)
3. Die drei Gleichungen als LGS aufstellen
I: -7 + r1·5 = 4 + r2·3 → 5·r1 - 3·r2 = 11
II: -3 + r1·3 = -6 + r2·5 → 3·r1 - 5·r2 = -3
III: -8 + r1·(-1) = -6 + r2·(-2) → ... (es reichen I und II)
LGS lösen mittels der ersten 2 Gleichungen via LGS-Löser oder schriftlich.
Ergebnisse: r1 = 4 und r2 = 3
Aussage: Ein Schnittpunkt existiert.
4. Dieses Ergebnis in eine Geradengleichung einsetzen:
AB: (x|y|z) = (-7|-3|-8) + r1·(5|3|-1)
AB: (x|y|z) = (-7|-3|-8) + 4·(5|3|-1) = (-7+20| -3+12 | -8-4) = (13|9|-12)
S(13|9|-12)
5. 3D-Zeichnung via Geoknecht erstellen und Lösung grafisch prüfen!
Stimmt, hier 3D-Zeichnung aufrufen. Sieht so aus:
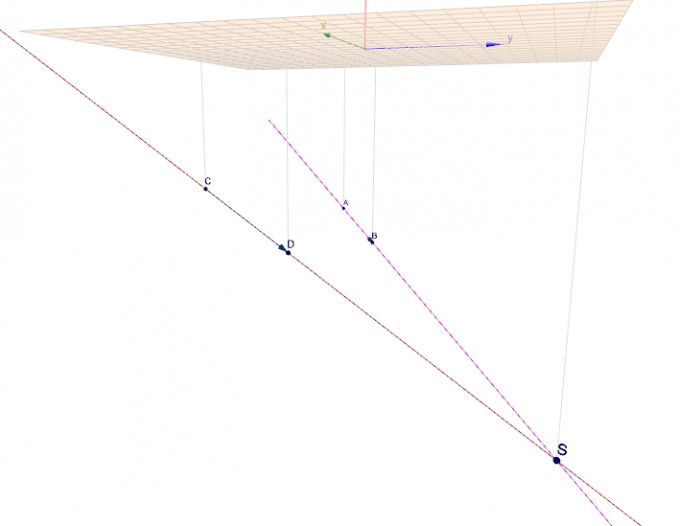
Hoffe, das hilft.