Geben Sie o:= o1 ° o2 und r:= o2 ° o1 als Produkt von unabhängigen Zyklen an.
das machen wir von rechts nach links.
Ich mach das zeichnerisch in der nun angegebenen Reihenfolge und komme auf:
o1 = (12)(34)(67)
Rot: Resultierende, wenn zuerst blaue und dann graue Verschiebung
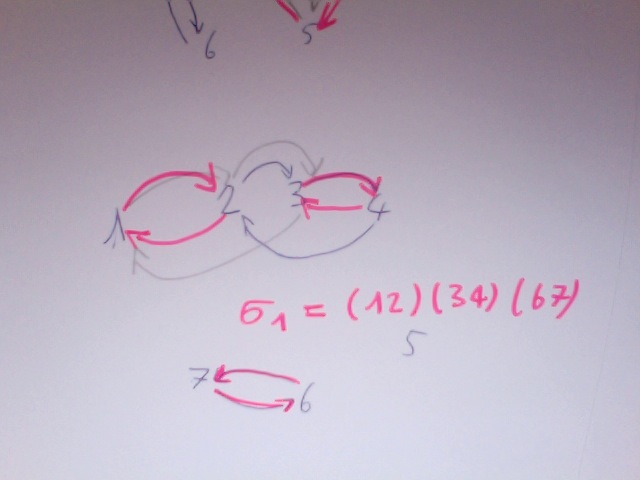
o = (14352)(67)
Rot: Resultierende, wenn zuerst graue und dann blaue Verschiebung
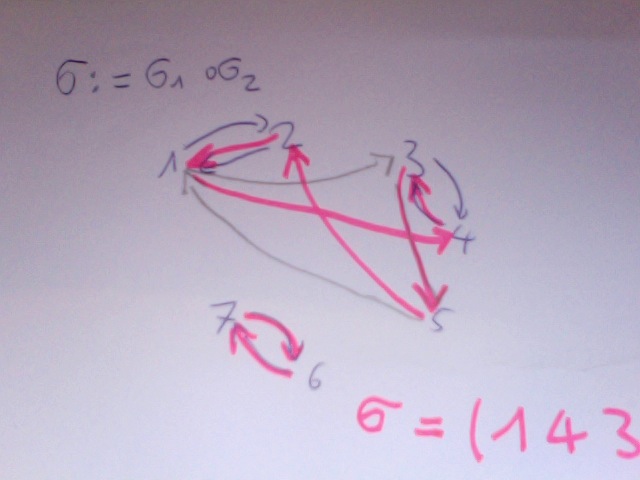
r = (12345)(67)
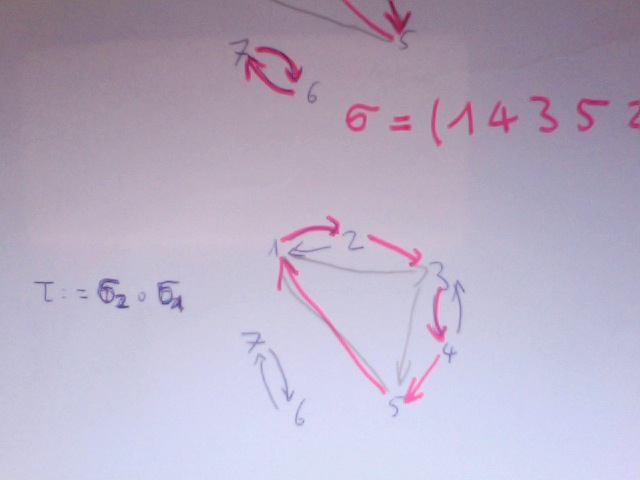
Rot: Resultierende, wenn zuerst blaue und dann graue Verschiebung