Hallo für die Aufgabe
soll man für diese 4 vektoren
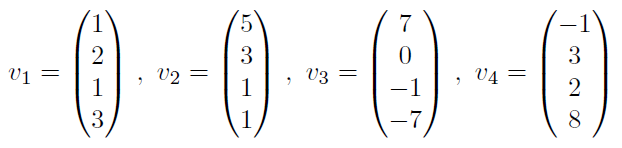 folgendes überprüfen :
folgendes überprüfen :
a) Uberprüfen Sie, ob das folgende Vektorsystem (v1, v2, v3) linear
unabhängig ist.
b)Wird die lineare Hülle größer, wenn wir noch den Vektor v4 dazunehmen?
bei a ) habe ich das Gaußverfahren angewandet um die beziehung λ1v1+λ2v2+λ3v3 =0 zu überprüfen dann wären diese vektoren linear unabhängig.
1 5 7 =0
2 3 0 =0
1 1 -1=0
jedoch ergab sich mal eine Nullzeile was dazu führte das ich λ3 frei wählen konnte und somit unedlich viele Lösungen erhalten habe .
x=λ3(3 -2 1) , wenn man hier die probe mit 3=λ1 , -2=λ2 und 1=λ3 macht kommt der 0-Vektor raus .
also linear abhängig.
bei b )habe ich das ganze nochmals um v4 ergänzt sodass sich für λ1v1+λ2v2+λ3v3+λ4v4 =0 die Matrix
1 5 7 -1=0
2 3 0 3=0
1 1 -1 2=0
3 1 -7 8=0
ergibt .
jedoch ergab sich wieder eine Nullzeile was dazu führte das ich λ3 frei wählen konnte und somit unedlich viele Lösungen erhalten habe .
x=λ3(3 -2 1 0) , wenn man hier die probe mit 3=λ1 , -2=λ2 , 1=λ3 und λ4=0 macht kommt der 0-Vektor raus .
also linear abhängig.
aber wie kann ich überprüfen ob die Lineare Hülle größer wird ?
Muss ich für L(v1,v2,v3) = L(v1,v2,v3,v4) die Summen
i=1 bis 3 ∑λivi = i=1 bis 4 ∑λivi vergleichen?
da kommt dann das gleich raus .
jedoch wiederspricht das dem Satz den wir aufgeschriben haben , insbesondere dem 2ten bzw. 3ten Punkt:

Kann mir da jemand das erklären wie sich diese Hülle ändert oder nicht?
Danke !