Monotonieverhalten mit Ableitungen

Question

ich möchte diese beiden Aufgaben lösen, habe dabei doch ein paar kleine Schwierigkeiten:

1.) 

Normalerweise haben wir die Nullstellen immer mit der pq-Formel ausgerechnet, wie geht das aber mit einer 3er Potenz? 

2.)

Es steht ja x > 0 da, was muss ich beim Rechnen dadurch jetzt beachten? Kann ich erst "ganz normal" ableiten?

Für jeden Tipp wäre ich dankbar, vielen Dank schon einmal im Voraus :)

Comments

Kann jemand weiterhelfen? :) Wäre wirklich sehr dankbar dafür.

Answer 1

Aufgabe 4.1) Wenn es um die Nullstellen geht, braucht man keine Ableitung. Wenn es um die Nullstellen der ersten Ableitung geht, macht man so weiter

4x³+2x=0 (deine letzte Zeile). Jetzt folgt Ausklammern

2x·(x²+1)=0. Ein Produkt ist 0, wenn ein Faktor 0 ist. Lösungen ergeben sich danach für

2x=0 (also x=0) oder für x²+1=0 (also für x² = - 1, was ja in den reellen Zahlen nicht möglich ist).

Einzige Nullstelle der ersten Ableitung ist also x=0.

Über die Monotonie sagt das aber nichts. Hier müsste man die Ungleichungen 4x³+2x>0(streng monoton steigend) und 4x³+2x<0(streng monoton fallend) untersuchen.

Comments

Vielen Dank für die Antwort! 
Ich verstehe nur nicht ganz die Sache mit dem Ausklammern.  Ich dachte es wären 2x·(2x²+1)=0 oder liege ich da komplett falsch?Und wissen Sie zufälligerweise etwas zu der 2. Aufgabe?Danke schon einmal :)

---

Du hast recht: Ausklammern ergibt 2x(2x²+1). Das Ergebnis ist dennoch richtig. Zur zweiten Aufgabe: Wenn es um die Nullstellen der ersten Ableitung geht, muss die Funktionsgleichung erst einmal bestimmt werden. Dazu schreibt man f(x)=x+x^-1. Dann ist f '(x)= 1 - 1^-2 oder f ' (x)  = 1-1/x². Die Gleichung 0 = 1-1/x² formt man um in x² = 1. dann sind die Lösungen x_1/2 = ±1.

Answer 2

zu 4.1

Für die Monotonie musst du hier keine Ungleichungen untersuchen:

f' '(x)  = 4x³ + 2x  = 0    ⇔  x=0  hast du ja schon.

da die Funktion f '  in ℝ stetig ist, kann sie ihr Vorzeichen nur an ihren Nullstellen ändern. 

Deshalb kannst du mit 2 Einsetzungen in die Funktion f '  deren Vorzeichenverlauf und damit die Monotonieintervalle bestimmen:

x         - ∞               -1                         0                              1                    ∞                 

f '(x)                        -6                         0                             6

f                   s.m. fallend             Tiefpunkt              s.m. steigend

                       ] - ∞ ; 0 ]                                                 [ 0 ; ∞ [  

zu 4.3

> Es steht ja x > 0 da, was muss ich beim Rechnen dadurch jetzt beachten? Kann ich erst   "ganz normal" ableiten?

Ja.   x>0  gibt den Definitionsbereich an und macht das Rechnen einfacher. 

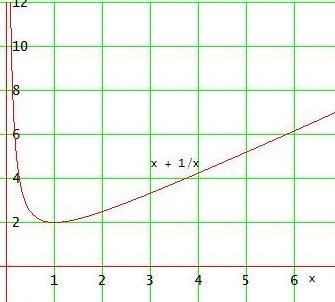
f(x) = x + 1/x   →   f '(x) =  x - 1/x²  

x - 1/x²  = 0   | * x² 

x³ - 1 = 0

x³ = 1

x = 1  

x           0                1/2                        1                               2                    ∞                 

f '(x)                        -3                          0                             3/4          

f                   s.m. fallend             Tiefpunkt              s.m. steigend

                        ] 0 ; 1 ]                                                    [ 1 ; ∞ [  

Gruß Wolfgang