Welche Höhe wird mit Rampe überwunden? (Sinus und Kosinus)

Question

Eine Rampe für Rollstuhlfahrer ist 4.50 m lang. Der Neigungswinkel beträgt 3.4°

Welche Höhe wird mit Rampe überwunden?

B. Die Neigung einer Rampe für Rollstuhlfahrer beträgt laut Bauvorschrift maximal 6%

Wurde diese Bestimmung in Teilaufgabe  a) eingehalten?

C) eine Rampe für Rollstullfahrer soll höchstens 6 m lang sein

Welche Höhe kann damit erreicht werden.

Answer 1

Hallo Girly,

A)

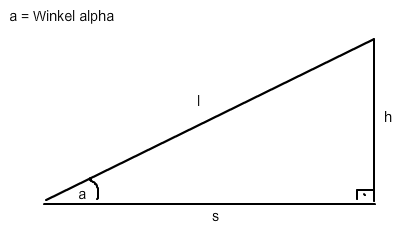
i = 4,50 m  ;  α = 3,4° ; h = ?

sin(α) = h / i  →  h = l * sin(α)  = 4,5m * sin(3,4°) ≈  0,267 m = 26,7 cm

B)

cos(α) = s / i  → s = l * cos(α) = 4,5 m * cos(3,4°)  ≈ 4,49 m 

Neigung = tan(α) = h / s = 0,267m / 4,49 m ≈ 0,059 = 5,9 % < 6 %

Die Bestimmung wurde also eingehalten.

Nachtrag:

C)

i_max = 6m  ;  maximale Neigung = 6% =  tan(α_max)  ;  h_max = ?

tan(α_max) = 0,06  →  α_max =  3,43°

in(α_max) = h_max / l_max  →  h_max = l_max * sin(α_max)  ≈ 0,359 m = 35,9 cm 

Gruß Wolfgang

Comments

Warum ist nicht s=4,5m es heißt doch die Rampe ist 4,50m lang? Ist das nicht ein wenig verwirrend, weil man kann das ja auf beiden Arten verstehen.

---

Die Rampe ( = Fahrweg) ist 4,5 m lang und das ist l

Answer 2

Hi,

eine Skizze vorab:

Bei uns ist gegeben die Länge der Rampe x. Zudem haben wir den Winkel zwischen z und x.

Damit können wir die Höhe y berechnen:

sin(a) = y/x

y = sin(a)*x = sin(3,4°)*4,50 m = 0,267 m

Es werden also etwa 26,7 cm mit der Rampe überwunden.

B)

m = tan(a) = tan(3,4°) = 0,059 = 5,9 %

Ja, wurde gerade eingehalten.

C)

Wir nehmen m = 6% = 0,06 = tan(a) --> a = 3,43°

Dann berechnen wir nun y über y = sin(a)*x = sin(3,43°)*6 m = 0,359 m

Es können also knapp 36 cm überwunden werden.

Grüße