Nullstellen von Funktionen mit höheren Potenzen

Question

ich versuche die Nullstellen von folgenden Funktionen zu finden:

a.) f(x) = -x^4 + 5x^2 -4

Ausklammern geht ja wegen der -4 nicht, ich hatte es versucht mit z = x^2 die pq-Formel zu benutzen, aber ich kam bloß auf 2 Nullstellen und nicht auf 4 wie es in der Lösung steht.

b.) f(x) = x^3-x^2-x-1

Gibt es noch einen anderen Weg als die Polynomdivision?

c.) f(x) = 1/8(x^4-x^3+2)

:)

Comments

(b)  \(x^3-x^2-x-1=0\). Substituiere \(x=\large{\frac{u+1}3+\frac4{3u}}\) und erhalte \(\left(u^3-19\right)^{\!2}=297\). Berechne daraus \(u\) und damit \(x\).

Answer 1

a.) f(x) = -x⁴ + 5x² -4

Ausklammern geht ja wegen der -4 nicht, ich hatte es versucht mit z = x² die pq-Formel zu benutzen,

Gute Idee!!!

 aber ich kam bloß auf 2 Nullstellen und nicht auf 4 wie es in der Lösung steht.


z=4  oder z=1   Jetzt wieder rückgängig machen


x² = 4  oder  x² = 1 also


x=2 oder x=-2  oder x=1  oder x= -1

b.) f(x) = x³-x²-x-1

Gibt es noch einen anderen Weg als die Polynomdivision?

Ja, ist aber recht aufwändig:  Cardano-Formel ( Google mal)


oder näherungsweise (Newtonverfahren) oder du hast vielleicht bei einem


der drei Minuszeichen in Wirklichkeit ein plus ???

c.) f(x) = 1/8(x⁴-x³+2)   Du kannst ja von  x⁴-x³+2  die

Extrempunkte bestimmen und findest :


Das absolute Minimum ( bei x=0,75 ) hat einen pos. y-Wert.

Also gibt es keine Nullstellen.

Answer 2

a.) f(x) = -x⁴ + 5x² -4 hier setzt man x²=z und löst die Gleichung -z²+5z-4 =0. Danach macht man die Substitution wieder rückgängig.

b.) f(x) = x³-x²-x-1

Gibt es noch einen anderen Weg als die Polynomdivision?

Auch die Polynomdivision wrd hier schwierig.

c.) f(x) = 1/8(x⁴-x³+2) Hier geht mit Standardmethoden gar nichts mehr.

Bist du bei b) und c) sicher, dass alle ±Zeichen so stimmen?

Comments

Erst einmal danke, und ja, ich habe eben gerade nochmal nachgeschaut und die ± Zeichen stimmen alle :)

Answer 3

zu a): nach der Rücktransformation ergibt das

x² = konst. | Umkehrfunktion: ±sqrt(x) also positive und negative Wurzel

x = ±sqrt(konst)

so kommt man auf die 4 Lösungen

zu b) und c):

die Geschichte spiegelt sich in den Klassenstufen wieder:

- bis zur Klasse 10 werden nur leicht zu erratende Nullstellen abgefragt, damit man Polynomdivision oder Substitution anwenden kann

- wird es krumm, nimmt man ab 10. Klasse Bisektion (eine Art systematisches Probieren) oder Iterationsverfahren: Selbstiteration oder Newton-Verfahren (schnelle Iteration) für reelle Ergebnisse

- dann wurden schon 1545 die Formeln

https://de.wikipedia.org/wiki/Cardanische_Formeln

veröffentlicht, ABER noch Fallunterscheidung und sehr langer Weg...

- heute kennt man die exakten expliziten Lösungsformeln (PQRST für Grad 3 und PQRSTUVW Grad 4 mit komplexen Zwischenergebnissen -> kein Schulstoff!):

http://www.lamprechts.de/gerd/php/gleichung-6-grades.php

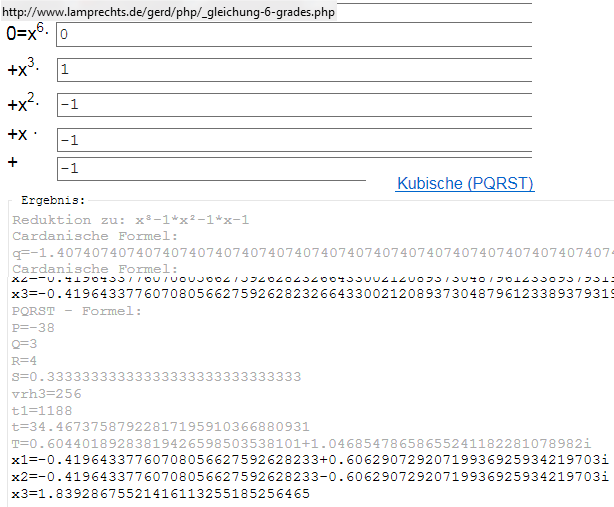
Für interessierte: x3=(1+(19-3*sqrt(33))^{1/3}+(19+3*sqrt(33))^{1/3})/3=1.839...  wie im Bild

Wenn Du also noch keine komplexen Zahlen hattest, hat c) keine reelle Lösung:

Der Faktor k=1/8 ist irrelevant, da k*0 = 0

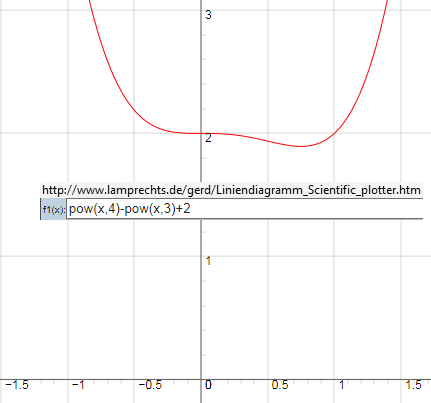
Polynom Grad n hat auch immer n Nullstellen, aber sie können auch:

- komplex

- doppelt (mehrfach übereinander liegend)

sein.

Wenn Ihr bei b) noch keine Näherungsverfahren hattet, hat sich bestimmt jemand (Lehrer oder Du) beim Abschreiben vertan...