Question

Die Gerade h enthält den Punkt P(4/5) und schliesst mit der Geraden g: 4x + 3y +6 = 0 einen Winkel von 45Grad ein. Gesucht ist die Gerade h in Koordinatenform. Ich versuche schon seit 2 Stunden es über das Skalarprodukt auszurechnen, aber vielleicht ist das der falsche Weg. Besten Dank schonmal!

Answer 1

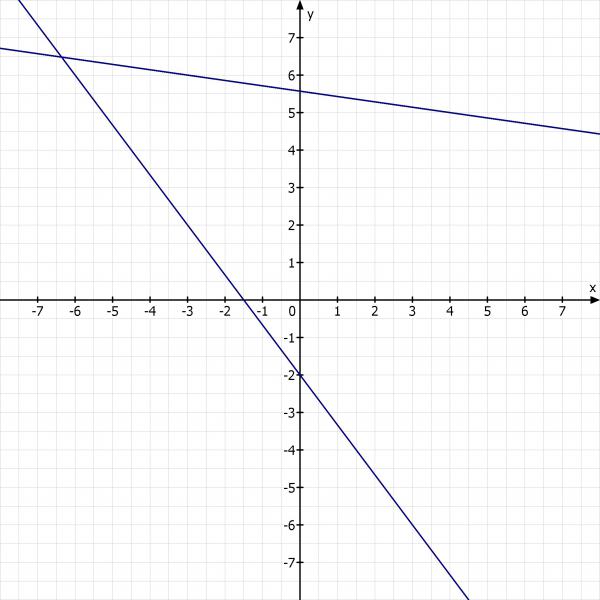
4x + 3y + 6 = 0
y = -4/3·x - 2 (Umwandlung nur für die Skizze)

Gegeben ist hier der Normalenvektor (4, 3). Daher hat unsere Gerade den Richtungsvektor (3, -4).

Die beiden Vektoren bilden allerdings einen 90 Grad Winkel. Da ich jetzt die Winkelhalbierende nutze addiere ich die beiden Vektoren

(4, 3) + (3, -4) = (7, -1) 

Das sollte dann der Vektor von meiner Geraden sein. Da der Punkt P(4|5) enthalten sein soll könnte ich die Punkt-Steigungsform aufstellen.

y = -1/7(x - 4) + 5 = 39/7 - x/7 bzw.

x + 7·y - 39 = 0

 

Skizze