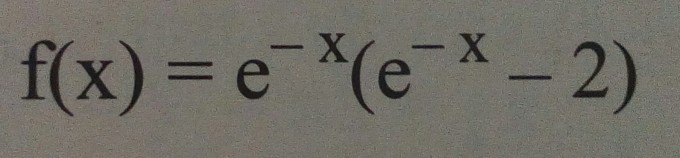Ich habe eine Funktion f(x)=e^{-x}(e^{-x}-2)
Die Aufgabe ist rechnerisch Achsenschnittpunkte, Asymptote, Extrempunkte und Wendepunkte herauszufinden.
Ich habe schon die Schnittpunkte
S(-0,68/0) S(0/-1)
Asymtote gibt es keine.
Aber bei Extremstellen komm ich nicht weiter.
Ableitung müsste f'(x)=-2e^{-2x}+2e^{-x}
Dann muss man zuerst diese auf Null setzten.
-2e^{-2x}+2e^{-x}=0 |÷2
e^{-2x}+e^{-x}=0 |ln
-2x+(-x)=ln0
Und das geht nicht, da aber ein Extrempunkt rauskommen müsste (ich hab getestet, dass wenn man x auf 0 setzt 0 raus kommt), muss ein Fehler drin sein und ich komm da nicht weiter (gleiches gold für Wendepunkte).
Hoffe jemand kann mir helfen.