Kurvendiskussion, Sylvesterrakete wird senkrecht nach oben geschossen.

Question

Eine Sylvesterrakete wird senkrecht nach oben geschossen.

Die erreichte Flughöhe in Meter nach t Sekunden wird durch die Funktion h(t)=-10t^2+80t erfasst.

a) wann erreicht ie Rakete ihren höchsten Punkt? welche hat sie dann erreicht?

habe h(4)=160

 erhalten, also erreicht die Rakte nach 4 Sekunden ihren höchten Punkt.

Stimmt das?

b) Wie schnell ist sie beim Start bzw. auf halber Gipfelhöhe?

h(0)= 0 -> Start

h (2)= 120 -> halbe Gipfelhöhe

Aber wie würde die Antwort lauten und stimmen die Ergebnisse?

Comments

a.) stimmt

b.) Auf- und Abstiegsteil der Parabel sind
symmetrisch.

nach 4 sec ist die Geschwindigkeit 0

Ich merke gerade

Stimmt die Formel ?

h(t)=-10t²+80t

Anfangsgeschwindigkeit 80  m / sec  ( nach oben )
Erdbeschleunigung -10 * t^2 ( nach unten )

müßte eigentlich -10 / 2 * t^2 ( g = 10 m / sec^2 )
s = 1/2 * g * t^2 sein.

Stimmt die Formel ?
Bitte einmal nachschauen.

---

h(t)=-10t²+80t ist die Funktion.

---

h(t)=-10t²+80t

h ´ ( t ) = v ( t ) = -20 * t + 80
v ( 0 ) = 80 m/s

In der Ausgangsformel ist die Anfangsgeschwindigkeit von 80 m/s
bereits angegeben.

Sylvesterraketen werden auf der Erde benutzt
Die Erdanziehung beträgt g = 9,.81 m/s^2
näherungsweise 10 m/s^2

Für die Erde muß die Formel

h ( t ) = -1/2 * g * t^2 + v0 * t
h ( t ) = -5 *t² + 80 * t

lauten. Andernfalls ist die Frage widersprüchlich und
macht es keinen Sinn.

---

ich habe die Aufgabe nochmals durchdacht und bin auch
bei mir auf Logikfehler gestoßen.
Eine Rakete beschleunigt ja, im Gegensatz zu einem
hochgeworfenen Stein, noch weiter.
Ich mache mir jetzt also keine Gedanken mehr um eine
physikalisch richtige Deutung des Bewegungssvorgangs
sonderen gehe einfach nach der angegebenen Formel vor.

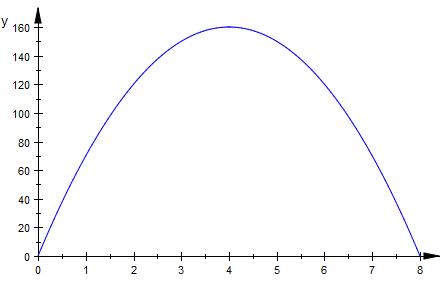
a) wann erreicht ie Rakete ihren höchsten Punkt?
welche hat sie dann erreicht?

Am höchsten Punkt ist die Geschwindigkeit = 0 m/s

h(t)=-10t²+80t

h ´ ( t ) = v ( t ) = -20 * t + 80
-20 * t + 80 = 0
t = 4 sec
h ( 4 ) = 160 m

Die Rakete erreicht ihren höchsten Punkt nach 4 sec.
Ihre Steighöhe ist dann 160 m.

b) Wie schnell ist sie beim Start bzw. auf halber Gipfelhöhe?

v ( 0 ) =-20 * 0 + 80
v ( 0 ) = 80 m/s

Die Geschwindigkeit beim Start beträgt 80 m/sec.

h(t)=-10t²+80t  = ( 160 / 2 )

-10t²+80t  = ( 160 / 2 )
t = 1.1716 sec

v ( 1.1716 ) = -20 * 1.1716 + 80
v ( 1.1716 ) = 56.568 m/s

Die Geschwindigkeit bei einer Höhe von 80 m beträgt
56.568 m/sec

mfg Georg

---

Ich bin am Anfang genau in der Art ungefähr vorgegangen. Da man ja 160m als Maximum hat -> Hälfte :80m

Hätte dann die Funktion

80= -10t²+80t 

und das ganze nach t auflösen können.

Bei der Nullstelle hätte ich doch auch die Funktion
h(t)=-10t²+80t Null setzen können oder nicht?

Der User Det hat vorgeschlagen, mit der ersten Ableitung voranzugehen.


h(t)=-10t²+80t

   

---

Du hast zunächst die Höhenfunktion.
siehe Skizze.

h ( t ) = -10t² + 80 * t

Daraus habe ich die Geschwindigkeitfunktion gebildet
erste Ableitung.

v ( t ) = -20 * t + 80

Die Geschwindigkeit ist die " Steilheit " der Kurve.
( oder Steigung )

Du siehst das die Steilheit bei h = 0 m am größten ist
und am höchsten Punkt gleich 0 ist.

bei a.) wird nach der Zeit bis zum Erreichen des Hochpunkts
gefragt bei v = 0. Dann kann mit t die Höhe berechnet werden.

bei b.) wird nach der Zeit bis zum Errreichen der Höhe h ( t ) = 80 m
gefragt. Die gefundene Zeit t wird dann eingesetzt in  die
Geschwindigkeitssfunktion
v ( 1.1716 sec ) =  56.57 m / sec.

Answer 1

a) ok

b) v(t)=ds/dt=dh/dt=-20*t+80

    v(0)=80

    v(2)=40

Comments

Verwendet man die erste Ableitung?

---

Ja

v=ds/dt ist die erste Ableitung des Weges nach der Zeit

---

Aber wieso verwendet man die erste Ableitung?

---

Die erste Ableitung entspricht der Steigung der Kurve.

Je mehr der Weg steigt, desto gröser ist die

Geschwindigkeit.

---

Achso, wieso hätte man denn nicht die Ausgangsfunktion gebrauchen können?

---

Die Ausgangsfunktion beschreibt die Höhe (Weg)

abhängig von det Zeit.

Die Ausgangsfunktion wird einmal abgeleitet =v.

(Die zweite Ableitung ist dann die Beschleunigung =a.)