Dreieck ABC: A(-16/8), B(9/-17), C(12/ y>0) ist rechtwinkelig mit rechtem Winkel in C. C(12/?). Inkreis?

Question

Ermittle die unbekannte Koordinate von C so, dass das Dreieck ABC

A(-16/ 8) B( 9/ -17) C ( 12/ y>0) rechtwinkelig mit rechtem Winkel in C ist.

Berechne den Flächeninhalt dieses Dreiecks und gib eine Gleichung des Umkreises an. Ermittle die Gleichung des Inkreises sowie die Koordinaten seiner Berührpunkte Ta, Tb und Tc . In welchem Verhältnis stehen die Flächeninhalte der Dreice ABC und Ta Tb Tc. ?!?!?

Answer 1

A[-16, 8], B[9, -17], C[12, y]

Die Vektoren AC und BC müssen demnach senkrecht sein bzw. deren Skalarprodukt muss Null sein.

AC = C - A = [12, y] - [-16, 8] = [28, y - 8]

BC = C - B = [12, y] - [9, -17] = [3, y + 17]

AC * BC = [28, y - 8] * [3, y + 17] = y^2 + 9·y - 52 = 0

y = 4 (und y = -13)

Der Flächeninhalt berechnen sich jetzt über

Fläche = 1/2 * |AC| * |BC| = 1/2 * |[28, 4 - 8]| * |[3, 4 + 17]| = 300

 

Schau zunächst ob du das hier nachvollziehen kannst und ob du damit dann auch den Rest bearbeiten kannst.

Comments

wie kommst du auf 52 ?? und wie kommst du auf y= 4 bzw. -13 ich hab versucht

bei 

y²+9y-52=0 

y herauszuheben

---

ich habe nun weitergerechnet um den Umkreis zu bekommen mein y = 9/2 mein x sollte nach Lösung 7/2 sein aber bei mir ist es 11/ 2 hab ich vl wiedermal einen Vorzeichenfehler ??

meine Daten

 

AB 25 -25

BC 3  21

A+B /2=   -7/2 -9/2 

B+C/2 =   21/ 2 -13/2

 

dann habe ich meine Gleichungen aufgestellt

25x-25y =25 diese mit 25 gekürzt

3x+21y=-105 diese mit 3 gekürzt

 

dann bleibt mir 

x-y=1

x+7y= -35 diese hab ich minimiert

ich erhalte -8y=36

y=36/8 = 18/4 = 9/2 dann wollte ich ich die Gleichung x-y=1 mein 9/2) einsetzen und es kommt 11/2 raus was stimmt nun meine Lösung oder 7/2 ???

---

ich habe einfach 7/2 genommen und versucht den Radius auszurechnen. Ergebnis : wieder falsch :(

(x-xm)²+ (y-ym)²=r2

(-16 - 7/2)² + (8- 9/2)² = r²

256 + 224/2 + 49/2 +64 -144/2 + 81/2 = r²

425= r²

 

das kann nicht stimmen in der Lösung ist r²=312,5

 

den Inkreis muss man auch berechnen und die Tangenten wie berechne ich die Tangenten??

---

Ich werd wahnsinnig jetzt habe ich zum 3ten mal versucht die Tangene zu berechnen und ich schaffs nicht

bin so vorgegangen:

X= A+t*AC

 und die andere X*AC = I*AC

meine Gleichungen dazu sind x-7y= 72 und 7x-y=30 diese habe ich mit 7 multipliziert

mein x ist 69/ 24 das kann nicht stimmen :((((((((((((

---

Fange ich mal bei der ersten Frage an

[28, y - 8] * [3, y + 17] = 28 * 3 + (y - 8) * (y + 17) = 84 + (y^2 + 17y - 8y - 136) = y^2 + 9y - 52

 

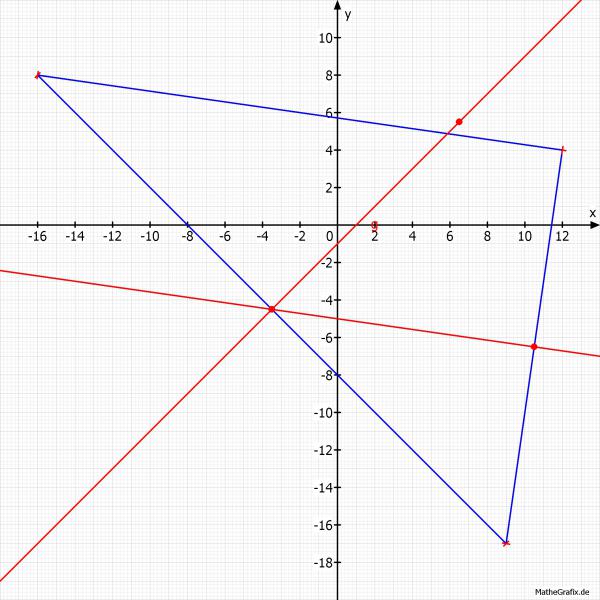
A[-16, 8], B[9, -17], C[12, 4]

Mittelpunkt des Umkreises ist der Schnittpunkt der Mittelsenkrechten

Mittelpunkt AB 
MAB = 1/2 * (A + B) = ([-16, 8] + [9, -17]) = [-3.5, -4.5]

AB = B - A =  [9, -17] - [-16, 8] = [25, -25]
Dazu senkrecht ist [1, 1] weil das Skalarprodukt 0 wird

Mittelsenkrechte von AB

[-3.5, -4.5] + r * [1, 1]

Genauso macht man die Mittelsenkrechte von BC

[10.5, -6.5] + s * [7, -1]

 

Schnittpunkt der Mittelsenkrechten

[-3.5, -4.5] + r * [1, 1] = [10.5, -6.5] + s * [7, -1]
r = 0 und s = -2

[-3.5, -4.5] + 0 * [1, 1] = [-3.5, -4.5]

Das kommt auch mit einer Skizze gut hin

---

was sind den nun deine Koordinaten vom Inkreis ? r² sollte 50 sein

---

A[-16, 8], B[9, -17], C[12, 4]

AB = [9, -17] - [-16, 8] = [25, -25] 
normiert 1/√2 * [1, -1] 

AC = [12, 4] - [-16, 8] = [28, -4]
normiert 1/(5*√2) * [7, -1]

Winkelhalbierende bei A

(1/√2 * [1, -1] + 1/(5*√2) * [7, -1]) = [6·√2/5, - 3·√2/5] = k * [2, -1]

[-16, 8] + r * [2, -1]

BA = 1/√2 * [-1, 1]

BC = [12, 4] - [9, -17] = [3, 21]
normiert 1/(5*√2) * [1, 7]

Winkelhalbierende bei B

1/√2 * [-1, 1] + 1/(5*√2) * [1, 7] = [- 2·√2/5, 6·√2/5] = k * [- 1, 3]

[9, -17] + s * [- 1, 3]

Schnittpunkt der Winkelhalbierenden

[-16, 8] + r * [2, -1] = [9, -17] + s * [- 1, 3]
r = 10 ∧ s = 5

[-16, 8] + 10 * [2, -1] = [4, -2]

Skizze

---

was bedeutet diese zeile
(1/√2 * [1, -1] + 1/(5*√2) * [7, -1]) = [6·√2/5, - 3·√2/5]


warum hast du immer eine wurze stehen von wo bekommst du die wurzel ? da verste ich nicht ganz

---

und wie berechne ich die Tangenten und das Verhätnis ? @ Mahecoach du hast ja meinen Rechengang gesehen wie ich den Inkreis berechnen wollte. war das falsch oder hab ich nur einene Rechenfehler eingebaut?

---

und warum hast du bei deiner Skizze immer bei den Punkte A B und C eine Gerade bzw. Tangente gezeichnet. wie zeichnet man dm besten den Inkreis ein?

einfach von 4 -2 zu den Punken A B und C einen Strich ziechen ?

---

also die Tangenten habe ich doch nun selbst geschafft
ich bräuch nur wirklich eine Erklärung zur Berechnung des Inkreises auf meine Art als auch auf Ihr Art da wäre mir sehr stark geholfen. LG

---

AC * BC = [28, y - 8] * [3, y + 17] = y2 + 9·y - 52 = 0

y = 4 (und y = -13)


kann mir jemand diese Lösung berechnen wie ich genau auf 4 komme ??

---

Du hast eine quadratische Gleichung

 y² + 9·y - 52 = 0

Die kannst du mit pq-Formel lösen.

Das sind Grundlagen die Du bei matheretter.de mal wiederholen solltest, wenn du die nicht mehr weisst.

https://www.matheretter.de/mathe-videos