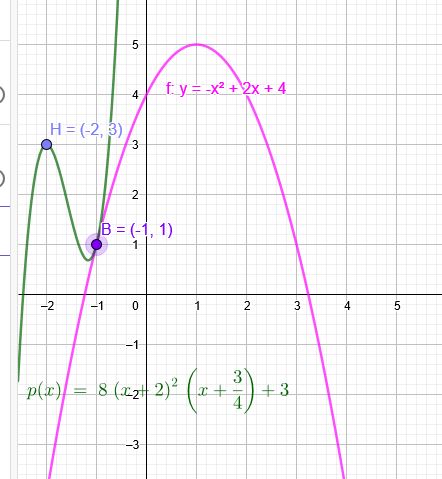
Geben sie die ganzrationale Funktion dritten Grades an, deren Graph einen Hochpunkt H\((-2|3)\) aufweist und die Parabel \(y=-x^2+2x+4\) an der Stelle \(x=-1\) berührt.
H\((-2|3)\)↓ H´\((-2|0)\) doppelte Nullstelle .
\(f(x)=a[(x+2)^2(x-N)]\)
Die Parabel \(y=-x^2+2x+4\) muss nun auch um 3 Einheiten nach ↓ verschoben werden:
\(v(x)=-x^2+2x+4-3=-x^2+2x+1 \)
An der Stelle \(x=-1\) wird \(f(x)\) von der Parabel \(v(x)=-x^2+2x+1 \) berührt.
Dort beträgt die Steigung \(v'(-1)=4 \) :
\(f'(x)=a[(2x+4)(x-N)+(x+2)^2 \cdot 1]\)
\(f'(-1)=a[(-2+4)(-1-N)+(-1+2)^2]=a[-2N-1]\)
\(a[-2N-1]=4\)
\(a=-\frac{4}{2N+1}\):
\(f(x)=-\frac{4}{2N+1}[(x+2)^2(x-N)]\)
Berührpunktkoordinaten:
\(v(-1)=-(-1)^2+2\cdot(-1)+1=-2\)
B\((-1|-2)\):
\(f(-1)=-\frac{4}{2N+1}[(-1+2)^2(-1-N)]=-\frac{4}{2N+1}(-1-N)\)
\(-\frac{4}{2N+1}(-1-N)=-2\)
\(N=-\frac{3}{4}\):
\(a=-\frac{4}{2 \cdot (-\frac{3}{4})+1}=8 \)
\(f(x)=8(x+2)^2(x+\frac{3}{4})\) ↑
\(p(x)=8(x+2)^2(x+\frac{3}{4})+3 \)