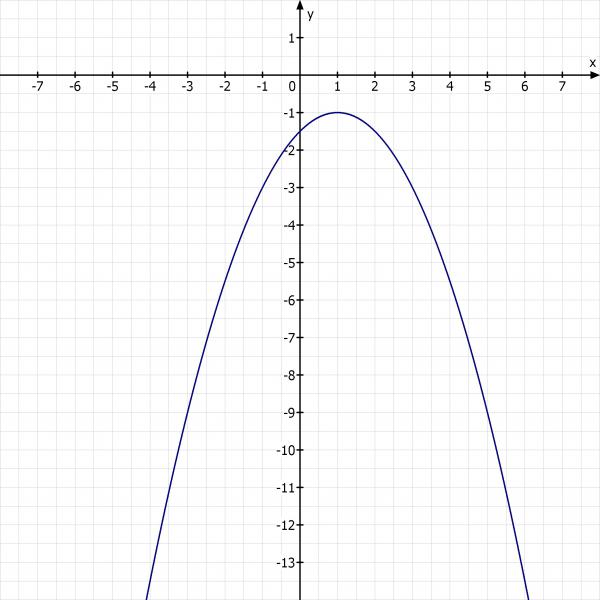
Von einer Parabel ist der Scheitel: (1|-1) bekannt. Außerdem liegt der Punkt (3|-3) auf der Parabel.
a) Gib die Gleichung der Parabel an. (Wie soll ich das machen, bitte ausführlich erklären)
Der Öffnungsfaktor a lässt sich bestimmen über
a = (Py - Sy) / (Px - Sx)^2
Dabei ist S(Sx|Sy) der Scheitelpunkt und P(Px|Py) ein weiterer Punkt der Parabel
a = (-3 - (-1)) / (3 - 1)^2 = (-2) / (2)^2 = -2/4 = -1/2
Jetzt stellt man die Scheitelpunktform auf
f(x) = a * (x - Sx)^2 + Sy = -1/2 * (x - 1)^2 - 1 = -1/2 * (x^2 - 2x + 1) - 1 = -1/2*x^2 + x - 3/2
b) Was lässt sich anhand der Parabelgleichung ohne weitere Rechnung über die Parabel sagen?
Y-Achsenabschnitt ist bei -3/2. Die Steigung im Y-Achsenabschnitt ist 1. Die Parabel ist nach unten geöffnet und gestaucht.
c) Erstelle eine Wertetabelle und zeichne die Parabel
Ich lasse mal die Wertetabelle. Die kannst du sicher selber leicht erstellen. Die Zeichnung sollte etwa so aussehen: