Ist Tangente t: y=-3x+13 zugehörig zum Graphen?

Question

Folgende Aufgabenstellung: Die Gerade t mit der Gleichung y=-3x+13 ist Tangente an den Graphen der Funktion f mit f (x)=x^3-9x^2+24x-14. 

Weise dies nach 

Also, ich bin mir bewusst, dass eine Tangente dieselbe Steigung in einem Punkt hat wie der in Beziehung stehende Graph. Muss Ich nun die Ableitung bilden und einsetzen? Und was dann? 

Ich wäre sehr erfreut, wenn man mir irgendwie helfen könnte. 

Answer 1

Du kannst f '(x) = -3 (quadratische Gleichung) nach x auflösen. 

---> x1 und x2

Und dann f(x1) ausrechnen und mit y = -3x1 + 13 vergleichen. Dasselbe für x2, wenn bei x1 nicht das gleiche Resultat rausgekommen ist. 

Answer 2

Du leitest die Funktion ab. Die ableitung gibt dir ja die steigung an. Dann setzt du die ableitung gleich mit -3, denn das ist die steigung der tangente. Aufgelöst bekommst du vermutlich 2 x Werte. Diese musst du in die Funktionsgleichungen der ausgangsfunktion und der tangente einsetzen und schauen, ob du die gleichen y Werte rauskriegst. Wenn dies der Fall ist, dann ist die vorliegende geradengleichung auch eine Tangenten gleichung.

Answer 3

Ich habe mit x₀=3 gerechnet, dann kommt es hin.

Comments

Das ist bis jetzt die beste Antwort. Muss Och noch einmal umändern!

Answer 4

Ganz mathematisch

Für einen Berührpunkt Funktion und Tangente gilt

f ( x ) = t ( x )          [ gleicher Punkt - Schnittpunkt
f ´( x ) = t ´( x )       [ gleiche Steigung

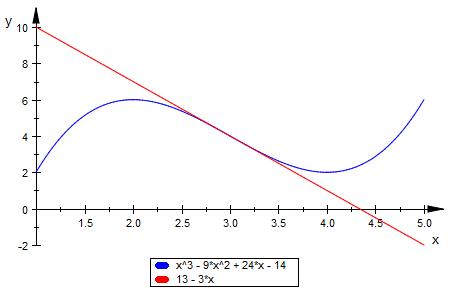
Folgende Aufgabenstellung: Die Gerade t mit der
Gleichung y=-3x+13 ist Tangente an den Graphen
der Funktion f mit f (x)=x³-9x²+24x-14.

f ( x ) = x³ - 9x² + 24x -14
f ´( x ) = 3 * x^2 - 18 * x + 24

t ( x ) = - 3x + 13
t ´( x ) = -3

f ´( x ) = t ´( x )       [ gleiche Steigung ]
3 * x^2 - 18 * x + 24 = -3
x = 3

f ( x ) = t ( x )          [ gleicher Punkt - Schnittpunkt
f ( 3) = 3³ - 9*3² + 24 * 3 -14 = 4
t ( 3 ) = - 3 * 3 + 13 = 4
B ( 3 | 4 )