Wie komme ich auf dieses Ergebnis? Änderungsrate

Question

Hi, ich versteh nicht wie diese Lösung entsteht, und bräuchte den rechen Weg. Und bitte nicht all zu kompliziert erklären.

Änderungsrate von f mit f(x) = 1/4x² - x + 1

auf [1; 1,5]

die Lösung wäre $$ \frac { f(1,5)-f(1) }{ 1,5-1 } $$ = -0,375

Wie kommt ich auf diese Lösung

Answer 1

Die Änderungsrate einer Funktion f(x) auf einem Intervall [x₁; x₂ ] ist \( \frac{f(x_2) - f(x_1)}{x_2 - x_1} \). Das ist einfach die Formel für die Steigung einer Geraden durch zwei Punkte und sollte noch vom Steigungsdreieck bekannt sein, vielleicht in der Form \( m = \frac{y_2 - y_1}{x_2 - x_1} \). Auswendiglernen!!!

f(x₂) berechnest du, indem du im Funktionsterm von f das x durch  x₂ ersetzt. Beispiel. f(x) = 1/4x² - x + 1. Dann ist f(8) = 1/4·8² - 8 + 1 = 9.

Comments

Bedeutet das, dass ich bei dieser Art von Aufgaben immer den gegebenen Grafen zeichnen muss?

Dann in der Aufgabenstellung ist tatsächlich kein Graf gegeben.

---

Es reicht, wenn du Schritte 1, 2 und 3 im Kopf ausführst.

---

Das sagt sich so leicht. ☺Trotzdem danke

---

Verstehst du den Zusammenhang zwischen \( \frac{f(1,5) - f(1)}{1,5 - 1} \) und der -0,375?

---

Das Ergebnis ist doch die Änderungsrate. Bloß kann ich mir nicht vorstellen das ich, um das Ergebnis zu erlangen, einen Grafen im Kopf zeichnen müsste.

Das würde mich sehr überfordern.

---

Ich habe meine Antwort etwas überarbeitet. Ich hoffe du kommst damit besser zurecht.

---

Vielen dank, auf jeden Fall jetzt verständlicher. Nur noch eine Frage. Ist die 8 die sie Einsetzen nur hypothetisch um mir das Beispiel zu verdeutlichen?

---

Die Frage hat sich erübrigt, ich habe es nachgerechnet. Sie haben mir sehr geholfen. Vielen Dank, nun hab ich das verstanden.

---

Du musst nicht im Kopf den Graphen zeichnen. Das könnte wohl kaum einer so ohne weiteres. Es reicht wenn du dir die Formel merkst die Oswald oben aufgeschrieben hat und dann mit Hilfe der Funktion 2 Funktionswerte ausrechnest damit du die 4 Werte in die Formel einsetzen kannst.

---

Kommentartext siehe unten

Answer 2

Vielleicht doch einmal eine Erklärung mit Bild

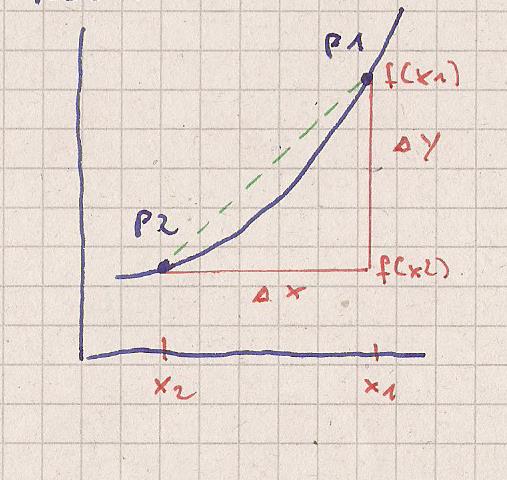
Du hast eine x-beliebige Funktion f.
Ein Punkt hat die Koordinaten ( x | y )

An der Stelle x1 ist der Funktionswert f ( x1 )

P1 ( x1 | f ( x1 ) )
P2 ( x2 | f ( x2 ) )

Die Änderung Δ y = f ( x1 ) - f ( x2 )
Die Änderung Δ x = x1  - x2

Die Änderungsrate ist
m = Δ y / Δ x
und entspricht  der Steigung der grünen gestrichelten Geraden.

m =  Δ y / Δ x =  [ f ( x1 ) - f ( x2 ) ]  /  ( x1 - x2 )

In deiner Aufgabe ist am einfachsten den Funktionswert
zunächst auszurechnen

P1 ( x1 | y1 )
P2 ( x2 | y2 )

Die beiden Punkte werden als Punkte auf einer Geraden
aufgefasst und dann berechnet mit

m = ( y1 - y2 ) / ( x1 - x2 )
( wie bei einer normalen Geradengleichung )

Comments

Gut Erklärt und Ordentlich hingeschRieben, Grüße!

---

Hallo Kofi,

(* Scherzmodus an *)
Gut Erklärt und Ordentlich hingeschRieben, Grüße!
besser
Gut erklärt und ordentlich hingeschrieben, Grüße!
(* Scherzmodus aus *)

---

Oh da haben heute mich wohl vertippt. ;-)

---

Mit am besten sind immer noch die Stilblüten
aus der Mathelounge

F(x)=e^-x*x2 der koordinatensprung der punkt p(u/0)
u der punlt q(u/f((u)) ,u>0 bilfen rechtwinköiges
dreieck ermittle u , für welchen der föächeninhal
des dreicks max ist.

Ich weiß, dass man immer für x das einsetzt gegen
was das laufen soll und wenn nicht 0 rauskommt
ist man fertig." 

Stimmt doch.

---

Und wenn ich schon einmal beim humorvollen
bin.

  Der Schachspieler Euwe fuhr mit dem Zug. Er kam mit seinem Gegenüber im Abteil ins Gespräch, ohne einander vorzustellen, und man beschloß zum Zeitvertreib Schach zu spielen.

  Im Laufe des Spiels machte sein Gegenüber einen nicht regelgerechten Zug, der dem Gegner auch einen Vorteil verschaffte. Trotzdem gewann Euwe das Spiel souverän.

  Der Gegenspieler dachte bei sich " wie ist das möglich das ich hier gegen jemanden verliere, der zudem die Regeln noch nicht einmal zu kennen scheint " und sagte zu Euwe

" Ich verstehe das nicht das ich hier so haushoch verliere. In meinem Verein gehöre ich mit zu den Besten. Im Verein nennt man mich den kleinen Euwe ".