Das große Dreieck lässt sich in die sieben Dreiecke PRQ, PQZ, QXZ, PYR, ZYP, RYX und QRX unterteilen.
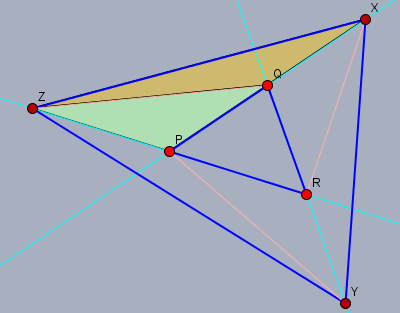
alle diese sieben Dreiecke haben den gleichen Flächeninhalt. PRQ (das ursprüngliche Dreieck) und ZPQ (grün) sind gleich, da ihre Grundseiten PR und ZP gleich lang sind und sie eine gemeinsame Spitze Q haben. Das Dreieck PQZ (grün) hat die gleiche Fläche wie QXZ (gelb), da wieder die Grundseiten PQ und QX gleich lang sind und die Spitze Z ist gemeinsam. Für die anderen Dreiecke lässt sich das ebenso zeigen. D.h. der Flächeinhalt von PRQ war 1176:7=168.
Das ganze kann man auch vektoriell zeigen. Sei \(PR=\vec{a}\) und \(PQ=\vec{b}\) so ist $$ZY=3 \vec{a} - \vec{b}$$ und $$ZX=\vec{a} + 2\vec{b}$$ Die Fläche von PRQ ist \(F=\frac{1}{2}(\vec{a} \times \vec{b})\). Die Fläche von ZYX ist dann $$F_7=\frac{1}{2}(3 \vec{a} - \vec{b}) \times (\vec{a} + 2\vec{b})= \frac{1}{2}(3 \vec{a}\times \vec{a} + 6\vec{a}\times \vec{b} - \vec{b} \times \vec{a} - 2\vec{b} \times \vec{b})=\frac{1}{2}(7\vec{a}\times \vec{b})=7 \cdot F$$