Hallo,
Woher weiß ich nun an welchem Punkt ich den zweiten Winkel PRQ ansetzen muss? Ich habe dort ja noch keinen festen Punkt an der Gerade die ich dank dem ersten Winkel zeichnen konnte.
Na ja es gibt da noch die Punkte \(P\) und \(Q\) und mehrere Möglichkeiten, um zur Lösung zu kommen. Die meiner Ansicht verbreiteste, läuft über den sogenannten Fasskreisbogen.
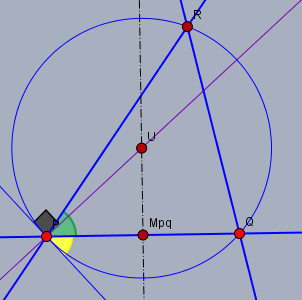
Die Strecke \(PQ\) (waagerecht) und den Winkel \(\angle QPR\) (grün) hast Du schon eingezeichnet.
Trage nun den Winkel \(\angle PRQ\) (gelb) im Punkt \(P\) unterhalb(!) der Strecke \(PQ\) ab. Konstruiere dann die Senkrechte (lila) zu dem Schenkel des Winkels in \(P\) und die Mittelsenkrechte (schwarz Strich-Punkt) der Strecke \(PQ\). Beide Geraden schneiden sich im Punkt \(U\). Der Kreis um \(U\) mit Radius \(|UP|\) schneidet den Schenkel von \(\angle PRQ\) in \(R\).
Eine alternative Konstruktion sieht so aus: Du zeichnest den Winkel \(\angle QPR\) (grün) noch einmal in \(Q\) an.
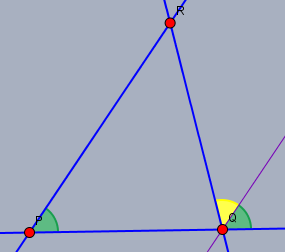
Sein Schenkel (lila) läuft zwangsläufig parallel zum Schenkel des Winkels \(\angle QPR\) in \(P\). Dann trägst Du den Winkel \(\angle PRQ\) (gelb) an dem neuen Schenkel in \(Q\) ab. Der Schenkel dieses Winkels schneidet den Schenkel des Winkels aus \(P\) wieder in \(R\).
Gruß Werner