Also wir haben die parabel p1
y=-1/2x^2+5
Und eine parabel p2 die durch ihren Scheitel (3/-4) gegeben ist. Diese wollen wir nun erstmal mit hilfe der Scheitelpunktform darstellen.
y=(x-3)^2-4
=x^2-6x+5
Gesucht ist nach einem Dreieck aus dem Scheitel von p1 und den beiden nullstellen von p2. Also ermittelt wir jetzt den Scheitelpunkt von p1. Praktischerweise ist p1 bereits in der Scheitelpunktform gegeben. Der Scheitelpunkt ist S1 (0/5). Dann brauchen wir jetzt noch die Nullstellen von p2.
(x-3)^2=4
(x-3)=±2
x_12=±2+3
x1=5
x2=1
Nun also das Dreieck mit der Grundseite (5-1)=4 und der Höhe 5 (y Koordinate von S1) Ergibt
A=G*h/2=4*5/2=10
Jetzt brauchen wir die Schnittpunkte der beiden Parabeln. Dafür setzen wir sie gleich.
x^2-6x+5=-1/2x^2+5
1,5x^2-6x=0
x*(x-4)=0
Satz vom nullprodukt
x1=0
x2=4
Wir berechnen die zugehörigen y-werte mit p1.
y (0)=5 S1 (0/5)
y (4)=-1/2*16+5=-3 S2 (4/-3)
Nun basteln wir uns aus diesen beiden Punkten eine geradengleichung mit hilfe der zwei-punkt-form.
y=(y2-y1)/(x2-x1)*(x-x1)+y1
y=(-3-5)/(4-0)*(x-0)+5
=-8/4*x+5
=-2x+5
Jetzt muss man etwas nachdenken. Wir haben ja die gerade gebastelt aus zwei Punkten, von denen der eine der Scheitelpunkt von p1 ist. Dieser Punkt markiert mit seiner y Koordinate ja die Höhe unseres Dreiecks. Das bedeutet, dass sich an der Höhe nichts ändert. Vielmehr zerteilt die gerade die Grundseite des Dreiecks. Da sich die Höhe nicht ändert, müsste die gerade schon die Grundseite in zwei genau gleich große Hälften zerteilen, damit sie auch das ganze Dreieck halbiert. Da die Grundseite auf der x-Achse liegt und von 1 bis 5 reicht, müsste die gerade sie also bei x=3 schneiden. Wir prüfen, ob sie das tut.
y=-2x+5=0
2x=5
x=2,5
Nein sie tut es nicht. Das bedeutet die gerade halbiert das Dreieck nicht, sondern zerteilt es in zwei ungleich große Teile.
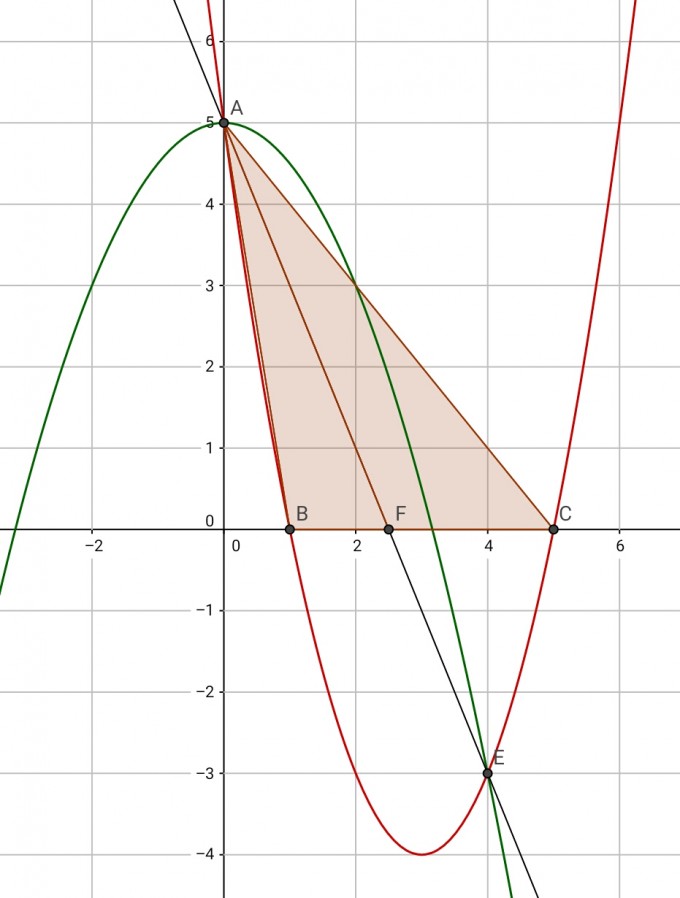
Nun noch die Grafik zur besseren Veranschaulichung.