Pythagoras: Seillänge in einer Turnhalle ausrechnen

Question

In einer Turnhalle hängt ein Kletterseil so, dassnoch 50 cm dieses Seil auf dem Boden liegen. Zieht man das untere Seilende 2,5m zur Seite, so berüht es gerade noch den Boden. Wie lang ist das Seil? Wie groß ist der Winkel, den das Seil dann mit dem Boden bildet?

Answer 1

Hi,

 

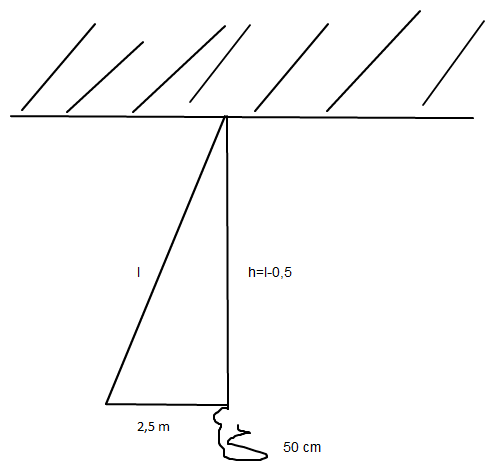
Das lässt sich nun mit dem Satz des Pythagoras lösen.

h^2+2,5^2=l^2=(l-0,5)^2+2,5^2

l^2=l^2-l+0,25+6,25  |-l^2+l

l=6,5

 

Das Seil hat also eine Länge von 6,5m. Die Halle (bzw, die Aufhängung) ist 6m hoch.

Der Winkel lässt sich beispielsweise mit dem cos berechnen.

cos(alpha)=2,5/6,5

alpha=67,38°

 

Grüße

Comments

kannst du mir auf deiner skizze zeigen wo die 2,5 m sind ?

---

Ich hatte vergessen sie einzuzeichnen. Ganz am Boden, denn dort wird ja das Seil auseinandergezogen ;).

Ich ergänze das mal.

---

ich versteh gar nicht wo das seil genug in der skizze befindet

---

@Nethan: Probier das mal mit einer Schnur oder einem Faden, den du an der Zimmerdecke oder über der Tür festmachst.

---

Das Seil komplett ausgezogen ist die lange Seite (Hypotenuse) welche mit l beschriftet ist.

Das Seil im hängenden Zustand ist mit h beschriftet. Der Überhängende Teil ist als etwas Gewursteltes direkt darunter gemalt und mit dem hinweis 50 cm versehen.


Nun deutlich? ;)

---

ja fast nur noch die 2, 5 m erklären bitte .. was hat es mut den seit zu tun

---

Du hast ein Seil herabhängen. Dabei entsteht ein Überschuss von einem halben Meter der lose auf dem Boden rumliegt.

Nun kommt ein Turner und nimmt sich das lose Seilstück. er läuft soweit, dass es kein loses Ende mehr am Boden gibt. Die Entfernung die er gelaufen ist beträgt 2,5m. Also nach 2,5m gibt es kein loses Ende mehr am Boden -> das Seil ist ausgestreckt und berührt gerade so den Boden.

---

super erklärt

---

hast du die binomische formel nicht falsch gerechnet?

---

Du darfst mich gerne korrigieren.

Wie kommst Du zu der Annahme? Was hättest Du anders gemacht?

---

(l-0,5)^2 ist doch falsch wiebdu gerrechnet hast oder

---

Dann rechne Du mal den Binom aus. Was erhältst Du? :)