Rekonstruktion und ich habe keinen Plan.

Question

Hey

Was soll ich denn mit der Informationen eine Funktion 3. Grades, deren graph symmetrisch zum ursprung ist und durch den Punkt P1 (1;-1) und P2 (-2;-16) verläuft anfangen? Wäre echt toll wenn mir da jemand helfen kann. Ich verstehe das Thema echt 0 und würde mich auch über einem link zu einem video oder einem Artikel zum Thema rekonstruieren von Funktionen freuen.

Danke

Answer 1

Was soll ich denn mit der Informationen eine
Funktion 3. Grades, deren graph symmetrisch
zum ursprung ist und durch den Punkt P1 (1;-1) und P2 (-2;-16) verläuft anfangen?

f ( x ) = a * x^3 + b * x^2 + c * x + d
Symmetrisch zum Ursprung
( 0 | 0 )
f ( 0 ) =  a * 0^3 + b * 0^2 + c * 0 + d = 0  => d = 0
f ( x ) = a * x^3 + b * x^2 + c * x
Symmetrisch zum Ursprung :
Punktsymmetrie => Nur ungerade Exponenten
f ( x ) = a * x^3 + c * x

f ( 1 ) = -1
f ( -2 ) = -16

f ( 1 ) = a * 1^3 + c * 1  = -1
f ( -2) = a * (-2)^3 + c * (-2) = -16

a  + c   = -1
-8 * a   - 2 * c  = -16

a  + c   = -1 | * -2

-2 * a - 2 * c = 2
-8 * a   - 2 * c  = -16 | abziehen
---------------------------
6 * a = 18
a = 3

a + c = -1
3 + c = -1
c = -4

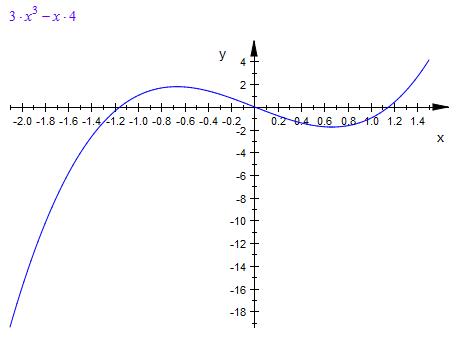
f ( x ) = 3 * x^3 - 4 * x

mfg Gold-und-Silber-lieb-ich