Zeige: die Ursprungsgerade h mit d. Steigung m=-3\4 berührt K.

Question

Fkt. vom Schaubild K ist f(x)=3\4(x^2-5x+4)

Wie kann ich den Berührpunkt von h und K herausfinden? 

Welche auf der Grd. h senkrecht stehende Grd. schneidet K in P(3|f(3))?Zeige: die Ursprungsgerade h mir d. Steigung m=-3\4 berührt K. 

Hoffe, dass mir da jemand helfen kann

Answer 1

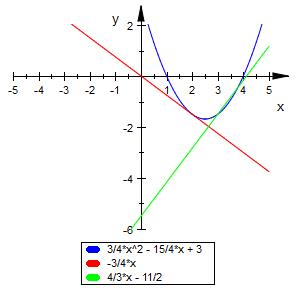
Fkt. vom Schaubild K ist f(x)=3\4(x²-5x+4)

Wie kann ich den Berührpunkt von h und K herausfinden? 

Welche auf der Grd. h senkrecht stehende Grd. schneidet K in P(3|f(3))?Zeige: die Ursprungsgerade h mir d. Steigung m=-3\4 berührt K.

Die Funktionen f und h berühren sich

Für einen Berührpunkt gilt
f ( x ) = h ( x )  | gleicher Punkt
f ´( x ) = h ´( x )   | gleiche Steigung

f ( x ) =3/4 * ( x² -5x + 4 )
f ´( x ) = 3/4 * ( 2x - 5 )

h ( x ) = -3/4 * x
h ´ ( x ) = -3/4

f ´( x ) = h ´( x )
3/4 * ( 2x - 5 ) = -3/4
2x - 5 = -1
x = 2

Die Funktion haben die gleiche Steigung bei x = 2
Probe ob auch Schnittpunkt
f ( 2 ) = h ( 2 ) Stimmt

Auf h steht eine weitere Gerade z als Normale.
Für die Steigung gilt
mz = -1 / mh
mz = - 1 / - 3/4
mz = 4 / 3

Ein Punkt auf z ist P (3 | f (3) )
P ( 3 | - 3/2 )

y = mz * x + b
-3 / 2 = 4 / 3 * 3 + b
-3 / 2 - 4 = b
b = - 11 / 2

z ( x ) = 4 / 3 * x - 11 / 2

Comments

Danke sehr jetzt kann ich auch nachvollziehen wieso :)

---

Gern geschehen.
Falls du weitere Fragen hast dann wieder einstellen.

---

Danke nochmals für die Hilfe... Hat lange gedauert aber ich habe es geschafft zu verstehen und zu lösen.

---

Schön das dir weitergeholfen werden konnte.
Es ist bekanntlich noch kein Meister vom Himmel
gefallen.
Durch das Lösen von Aufgaben und Problemen
lernt man am meisten.

Falls du weitere Fragen hast dann nachhaken
oder neu einstellen.

Answer 2

f(x)=3\4(x²-5x+4)       f ' (x) = 3/4  * (2x - 5 )

Zeige: die Ursprungsgerade h mir d. Steigung m=-3\4 berührt K. 


Wenn die sich berühren, haben sie in dem Punkt auch gleiche Steigung

3/4  * (2x - 5 )   =  -3/4

2x - 5 = -1

x = 2 .

Und der Punkt auf der Geraden hat y= -6/4  = -3/2und auf K gibt es bei x=3

f(3) =  3/4 * ( 4 - 10 + 4 ) =  -6/4 = -3/2

Passt also, ist der gleiche Punkt und beide haben

dort gleiche Steigung.  q.e.d.
 

Comments

Danke erstmal aber wie komme ich auf 3\4*(2x-5)

---

Das ist die Ableitung, also die Steigung von K.

Answer 3

Ursprungsgerade : h(x) = -3/4 x

f(x)=3\4(x²-5x+4)

Setze nun gleich und versuche aufzulösen.

"Welche auf der Grd. h senkrecht stehende Grd. schneidet K in P(3|f(3))?"

senkrecht, heißt dass wir eine gerade der Form: g(x) = -3/4x + b  haben.

Berechne nun f(3) und passe g(x) ( indem du b bestimmst) so an, dass f(3) = g(3) ist.