Basiswechsel bei ℝ-Vektorräumen ℝ^2 und ℝ^3 mit diesen Basen B und C?

Question

hallo mathelounge team, also ich habe folgende Aufgabe gegeben:

Ich habe die ℝ-Vektorräume ℝ² und ℝ³ und in diesen die Basen

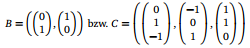
und die Standardbasen

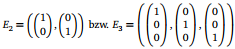
Eine lineare Abbildung ψ ∈ L(ℝ³ ,ℝ² ) ist gegeben durch  .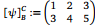

a) Ich muss nun 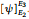 bestimmen.

Meine Ideen:

- muss ich einfach nur Basiswechsel vornehmen, also nur invertieren?

Danke schonmal für eure hilfe...

Answer 1

Du kannst es über die Basiswechselmatrizen machen oder "zu Fuß",

indem du die Bilder der Basisvektoren von E3 bestimmst, also etwa

    1                           0             -1                  1
f(  0  )   =  f (   -1/2*   1   -1/2 *  0    +1/2       1   )  =   -1/2 * 3    -1/2 *4   +1/2*5   =  -1
    0                          -1              1                  0                     1            2            3        0

Das wäre dann die erste Spalte der ges. Matrix.

Das andere ist aber wohl kürzer: 

0   1
1   0     mal die

gegebene Matrix * die Inverse von

0   -1   1 
1    0    1
-1   1   0

gibt dann

0     6     3
-1    3     2

Comments

hallo mathef,

danke für deine hilfe bei der a). Die a) konnte ich noch halbwegs verstehen. Nun brauche ich hilfe bei der b), die ich überhaupt nicht verstehe.

b) Gegeben sei weiterhin ein Vektor v∈ℝ³ durch .

Bestimme