Aufsuchen von Funktionen

Question

Vom Graphen einer Polynomfunktion 4. Grades y = a * x⁴ + b * x³ + c * x² + d * x+e sind folgende Eigenschaften bekannt:

Der Graph verläuft durch den Ursprung, Hochpunkt H₁ (-2/8) und H₂ (1/1,25)

Suche die Funktion

(Lösung: y= -0,75x⁴-x³+3x²)

Bitte erklären!!

Answer 1

y =  f(x)  =  ax⁴ + bx³ + cx² + dx + e

      f '(x)  =  4ax³ + 3bx² + 2cx + d

Bedingungen:

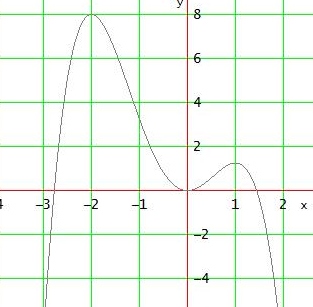
f(0) = 0    →  e = 0

f(-2)  =  16·a - 8·b + 4·c - 2·d  =  8

f'(-2) =  - 32·a + 12·b - 4·c + d  =  0

f (1)  =   a + b + c + d  =   1,25

f '(1) =   4·a + 3·b + 2·c + d  =  0  

Dieses LGS mit vier Gleichungen mit 4 Unbekannten musst du lösen (Gauß-Algorithmus).

.Dann erhältst du die Kontrolllösung.:  a = - 3/4  ;  b = -1  ;  c = 3  ;  d = 0  ;  e = 0

Gruß Wolfgang