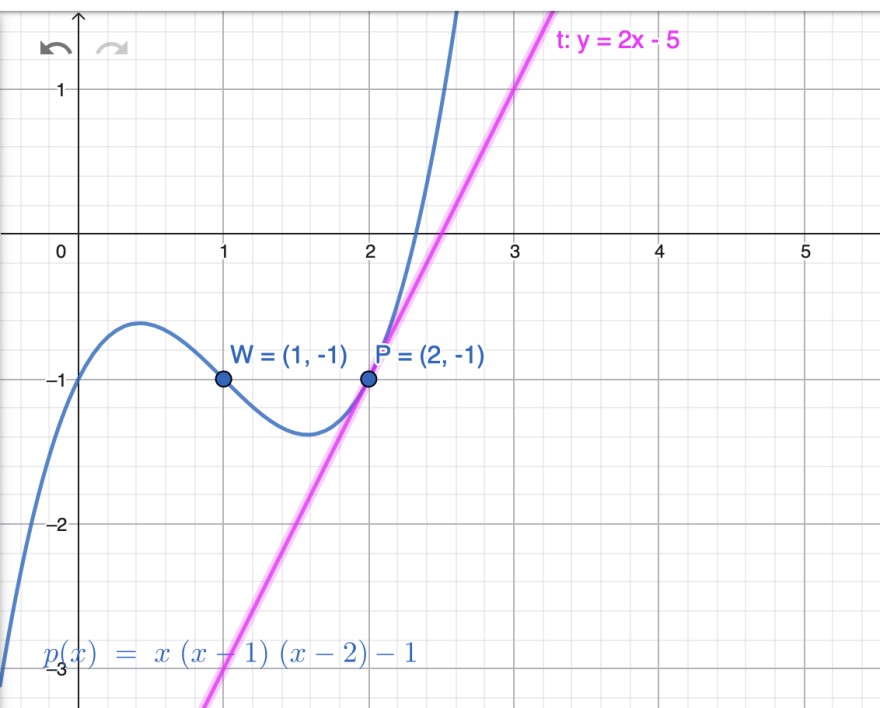
Eine Funktion dritten Grades hat den Wendepunkt W (1|-1) und im Punkt P (2|-1) den Anstieg k=2
Da die y-Werte von P und W gleich sind, verschiebe ich die um 1 Einheit nach oben. Somit ist an den Stellen x=1 und x=2 eine einfache Nullstelle.
Linearfaktorenform:
\( f(x)=a(x-1)(x-2)(x-N)=a(x^2-3x+2)(x-N)=a(x^3-Nx^2-3x^2+3Nx+2x-2N)\)
Wendepunkt W (1|-1). →2. Ableitung
\( f'(x)=a(3x^2-2Nx-6x+3N+2)\)
\( f''(x)=a(6x-2N-6)\)
\( f''(1)=a(6-2N-6)=0\)
\(N=0\)
\( f'(x)=a(3x^2-6x+2)\)
Anstieg k=2 → 1.Ableitung
\( f'(2)=a(12-12+2)=2\)
\( a=1\)
\( f(x)=x(x-1)(x-2)\)
...1 nach unten.
\(p(x)=x(x-1)(x-2)-1\)