Du weißt sicher, was der Tangens ist und Du kennst die Additionstheoreme für den Tangens. Dann kannst Du die Aufgabe auch lösen.
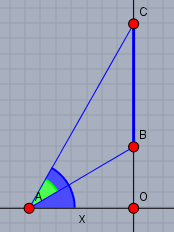
Das Bild liegt zwischen den Punkten B und C. Das Auge des Betrachers ist bei A und die waagerechte Entfernung sei \(x\). Die Strecke \(OB\) ist die Differenz zwischen der Bildunterkante und der Augenhöhe - also \(OB=2\text{m}-1,6\text{m}=0,4\text{m}\). Und \(OC\) errechnet sich aus \(OC=2\text{m}+0,8\text{m}-1,6\text{m}=1,2\text{m}\).Es gilt den Abstand \(x\) so zu wählen, dass der Winkel \(\alpha\) (hier grün) möglichst groß wird. Den blauen Winkel nenne ich \(\varphi\).
Wie Der_Mathecoach schon geschrieben hat, gilt jetzt
$$\tan{\varphi} = \frac{1,2}{x}$$
$$\tan{(\varphi - \alpha)} = \frac{0,4}{x}$$
Die letzte Gleichung kannst Du nun mit Kenntnis der Additionstheoreme umformen
$$\tan{(\varphi - \alpha)} = \frac{\tan {\varphi} - \tan{\alpha}}{1+ \tan{\varphi} \tan{\alpha}} = \frac{0,4}{x}$$
Setzte die erste Gleichung - also das \(\tan{\varphi}\) dort ein und nach einigen Umwandlungen erhält man
$$\tan {\alpha}=\frac{0,8x}{x^2+0,48}$$
Jetzt kommt ein Trick: Da A unterhalb von B liegt, kann \(\alpha\) in diesem Fall nie größer als \(90°\) werden. Und im Intervall von \(0\) bis \(90°\) gilt, dass der Tangens monoton steigend ist. Übersetzt bdeutet das, dass der Winkel \(\alpha\) genau dann möglichst groß wird, wenn sein Tangens möglichst groß wird. Also reicht es, den Tangens nach \(x\) abzuleiten
$$\frac{\delta \tan \alpha}{ \delta x}=\frac{0,8 \cdot \left( x^2 + 0,48\right) - 0,8x \cdot 2x}{\left( x^2 + 0,48\right)^2}$$
Nach Nullsetzen der Ableitung (hier reicht Nullsetzen des Zählers) erhält man \(x=\sqrt{0,48}=0,4\sqrt{3}\approx 0,6928\)