Extremwertaufgabe: optimale Entfernung einer Person, die Bild betrachtet

Question

ich komme mit folgender Aufgabe nicht zurecht:

Ein Bild ist so aufgehängt, dass Unterkante des Bildes 2 Meter über Boden ist. Bild ist 80 cm hoch. Ein betrachtende Person hat die Augenhöhe von 1,60 m.

Gesucht ist diejenige waagerechte Entfernung vom Bild, mit der der Beobachter vom Sehwinkel her das Bild am besten sieht.

Meine Überlegung: Die Person muss sowei vom Bild entfernt sein, dass sie das Bild ca. mittig betrachten kann. Aber wie gehe ich da matheatisch heran? Haupt-/Nebenbedingung?

Comments

Kann es sein, dass du den Winkel mit einer biologischen Recherche finden sollst?

https://de.wikipedia.org/wiki/Blickfeld

https://de.wikipedia.org/wiki/Sichtfeld

Hier scheint es allerlei "optimale Winkel" zu geben. Verfolge die Links in den angebenen Links und entscheide dich für einen Winkel.

NB. Wenn du Tangens gehabt hast, solltest du auch arctan kennen und benutzen können.

---

Den Tangens und den Arkustangens wurde bestimmt in dre Mittelstufe behandelt. Hier braucht man allerdings ja die Ableitung. Und da weiß ich nicht in wie weit diese durchgenommen worden war im Unterricht. Die Aufgabe stammt aber aus einem Buch. Und dann sollte man dazu eigentlich im Buch etwas finden.

Answer 1

Du weißt sicher, was der Tangens ist und Du kennst die Additionstheoreme für den Tangens. Dann kannst Du die Aufgabe auch lösen.

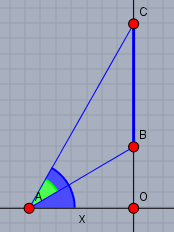
Das Bild liegt zwischen den Punkten B und C. Das Auge des Betrachers ist bei A und die waagerechte Entfernung sei $x$. Die Strecke $OB$ ist die Differenz zwischen der Bildunterkante und der Augenhöhe - also $OB=2\text{m}-1,6\text{m}=0,4\text{m}$. Und $OC$ errechnet sich aus $OC=2\text{m}+0,8\text{m}-1,6\text{m}=1,2\text{m}$.Es gilt den Abstand $x$ so zu wählen, dass der Winkel $\alpha$ (hier grün) möglichst groß wird. Den blauen Winkel nenne ich $\varphi$.

Wie Der_Mathecoach schon geschrieben hat, gilt jetzt

$$\tan{\varphi} = \frac{1,2}{x}$$

$$\tan{(\varphi - \alpha)} = \frac{0,4}{x}$$

Die letzte Gleichung kannst Du nun mit Kenntnis der Additionstheoreme umformen

$$\tan{(\varphi - \alpha)} = \frac{\tan {\varphi} - \tan{\alpha}}{1+ \tan{\varphi} \tan{\alpha}} = \frac{0,4}{x}$$

Setzte die erste Gleichung - also das $\tan{\varphi}$ dort ein und nach einigen Umwandlungen erhält man

$$\tan {\alpha}=\frac{0,8x}{x^2+0,48}$$

Jetzt kommt ein Trick: Da A unterhalb von B liegt, kann $\alpha$ in diesem Fall nie größer als $90°$ werden. Und im Intervall von $0$ bis $90°$ gilt, dass der Tangens monoton steigend ist. Übersetzt bdeutet das, dass der Winkel $\alpha$ genau dann möglichst groß wird, wenn sein Tangens möglichst groß wird. Also reicht es, den Tangens nach $x$ abzuleiten

$$\frac{\delta \tan \alpha}{ \delta x}=\frac{0,8 \cdot \left( x^2 + 0,48\right) - 0,8x \cdot 2x}{\left( x^2 + 0,48\right)^2}$$

Nach Nullsetzen der Ableitung (hier reicht Nullsetzen des Zählers) erhält man $x=\sqrt{0,48}=0,4\sqrt{3}\approx 0,6928$

Answer 2

α = ATAN((2 + 0.8 - 1.6)/x) - ATAN((2 - 1.6)/x)

α = ATAN(1.2/x) - ATAN(0.4/x)

α' = 20·(12 - 25·x²)/((25·x² + 4)·(25·x² + 36)) = 0 --> x = 0.6928

Die Person sollte eventuell 70 cm vor dem Bild stehen.

Comments

!

Könntest du noch die Idee hinter der Lösung nennen, also wie man genau auf den Ansatz mit arctan kommt?

---

Mal dir doch mal eine Skizze auf. Überlege was man mit dem ARCTAN berechnen kann. Überlege wie ich auf die Argumente im ARCTAN gekommen bin also was ich wohl berechnen möchte.

Natürlich könnte ich dir auch meine Skizze geben aber lernen tust du mehr wenn du sie dir selber anfertigst und überlegst.

---

Danke, eine Skizze hatte ich mir auch schon gemacht. Aber der Punkt ist, dass wir den arctan nicht behandelt hatten und deshalb wohl eine andere Lösungsweg gefragt ist. Was gibt es denn noch für Möglichkeiten?

---

Ich komme leider überhaupt nicht drauf. Ist alpha der Winkel, den die Person auf das Bild hat? Also so? Siehe Bild. Ich habe überhaupt keinen Ansatz für die Rechnung. Ich kann es ja nicht wie ein Dreieck berechnen, da zuviele Angaben fehlen. Oder?!

---

Beachte das das Bild höher hängt als die Sehhöhe ist. Zeichne also zwei Rechtwinklige Dreiecke. Von den Augen du den Bildkanten liegt die Hypotenuse. Waagerecht zur Wand die Ankathete. An der Wand hoch die Gegenkathete.

Der Blickwinkel (Sehwinkel) ergibt sich aus der Differenz der Winkel.

Eine andere Lösung als mit dem Arkustangens fällt mir dazu nicht ein. Wenn ihr den nicht gehabt habt solltest du dich darüber schlau machen. Eventuell steht dazu etwas im Buch auf den Seiten vorher.

Schau mal im Inhaltsverzeichnis.