Ganzrationale Funktion dritten Grades bestimmen, welche durch (0|0) läuft, ...

Question

Der Graph verläuft durch O  0/0  hat eint der Steigung -6

der Graph einen Hochpunkt H (-2/10)

wie ermittel ich jetzt den Funktionsterm der gesuchten Funktion ?

Answer 1

Hi,

stelle 4 Bedingungen auf, da Du mit der Funktion dritten Grades 4 Unbekannte hast: y=ax^3+bx^2+cx+d

Diese sind:

f(0)=0        (Durch Ursprung)

f'(0)=-6      (Steigung -6)

f(-2)=10    (Hochpunkt)

f'(-2)=0      (Bedingung für Hochpunkt)

 

Das ergibt das LGS:

d = 0
c = -6
-8a + 4b - 2c + d = 10
12a - 4b + c = 0

 

Dies löse (setze c=-6 und d=0 direkt ein) und erhalte: a=1, b=1,5 und c=-6, d=0

 

y=x^3+1,5x^2-6x

ist die gesucht Funktion dritten Grades.

Grüße

Comments

ok,aber was ist das LGS und wie kommt man darauf ? :)

---

Das ist ein lineare Gleichungssystem ;).

Du nimmst Dir also Deine Bedingungen und setzt sie in

f(x)=ax^3+bx^2+cx+d

und

f'(x)=3ax^2+2bx+c

ein.


Nun wieder klar? Sonst frage nach :).

---

aber um ein lineares Gleichungssystem zu lösen muss ich doch drei Gleichungen haben ,welche sind dann meine 3 Gleichungen und woher weiß ich nochmal was ich wo einsetzen muss ?

---

Es sind sogar 4 Gleichungen :).


d = 0
c = -6
-8a + 4b - 2c + d = 10
12a - 4b + c = 0


Diese hast Du erhalten, da Dir die Bedinungen bekannt sind:

f(0)=0        (Durch Ursprung)

f'(0)=-6      (Steigung -6)

f(-2)=10    (Hochpunkt)

f'(-2)=0      (Bedingung für Hochpunkt)


Nehmen wir mal das erste (Ursprung als Beispiel):

Es ist f(x)=ax^3+bx^2+cx+d

Nun wissen wir f(0)=0

a*0^3+b*0^2+c*0+d=0

Also d=0.

Die anderen Gleichungen werden genauso aufgestellt.

Alles klar?

Das dann noch lösen. Setze dafür direkt c und d ein. Dann hast Du nur noch zwei Gleichungen mit den Unbekannten a und b ;).

---

aber wieso wissen wir das das d ist und nicht zum Beispiel a ?

---

Das hatten wir festgelegt, in dem wir die Variablen zu y=ax³+bx²+cx+d bestimmt haben.

d ist die einzige Variable (im vorgerechneten Beispiel) die von der 0 unberührt bleibt. Deswegen bleibt alleine d=0 übrig.

---

bei der Steigung -6 muss ich doch jetzt erstmal die Ableitung bilden und dann  -6 für x einsetzen,oder?

---

Fast :).

Richtig ist, dass Du die Ableitung bilden musst.

Allerdings gibt die Ableitung die Steigung aus. Der y-Wert der Ableitung ist also -6.
Einsetzen musst die Stelle, an der die Ableitung -6 ist -> x=0.


Probier weiter :)

---

muss ich jetzt c und d in die  Gleichung -8a-4b-2c+d= 10 einsetzen;wenn ja wie genaulöse ich es nach a und b auf  ?

---

Das wäre mein Vorschlag. Genau! ;)

-8a + 4b - 2c + d = 10
12a - 4b + c = 0

Einsetzen von c=-6 und d=0

-8a+4b-2*(-6)=10  |-12
12a-4b-6=0            |+6

-8a+4b=-2
12a-4b=6


Willst Du es selbst probieren? Zwei Gleichungen mit zwei Variablen ;).

---

ja super jetzt habe ich es verstanden,vielen Dank ! :)

---

Haha, sehr gut!
Du hast dann also auch a=1 und b=1,5 rausgekriegt, wie ich es ganz oben vorgestellt hatte?

-> y=x³+1,5x²-6x

Sehr schön! Und gerne :).

Answer 2

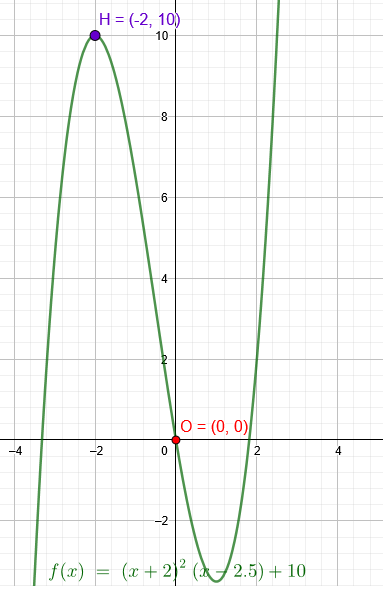
"Der Graph verläuft durch O (0|0)  hat dort die Steigung -6  der Graph einen Hochpunkt H (-2|10)"

O (0|0)→O´ (0|-10)     Hochpunkt H (-2|10)  →  Hochpunkt H´ (-2|0) doppelte Nullstelle

\(f(x)=a*(x+2)^2*(x-N)\)

O´ (0|-10)     \(f(0)=a*(0+2)^2*(0-N)\)     \(-4aN=-10→a=\frac{2,5}{N}\)

\(f(x)=\frac{2,5}{N}*[(x+2)^2*(x-N)]\)

\(f´(x)=\frac{2,5}{N}*[2*(x+2)*(x-N)+(x+2)^2]\)

\(f´(0)=\frac{2,5}{N}*[2*(0+2)*(0-N)+(0+2)^2]\)

\(f´(0)=\frac{2,5}{N}*[-4N+4]\)         \(\frac{2,5}{N}*[-4N+4]=-6\)         \(N=2,5\)      \(a=\frac{2,5}{2,5}=1\)

\(f(x)=(x+2)^2*(x-2,5)\)

\(p(x)=(x+2)^2*(x-2,5)+10\)

Comments

Endlich mal eine Antwort von Moliets auf diese 9 Jahre alte Frage eines Users, der schon lange nicht mehr Mitglied ist.

---

Es gibt möglicherweise User, die Steckbriefaufgaben durchsuchen und ein Aha-Erlebnis haben, wenn sie diese Lösungsart entdecken.