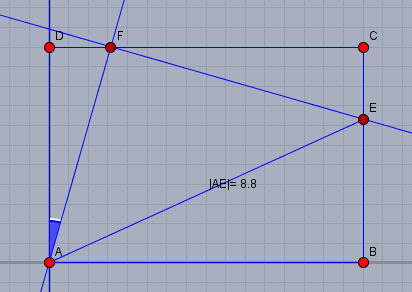
Die zweite Seite des Rechtecks folgt aus der Fläche \(AB=DC=44{\text{cm}}^2/5,5\text{cm}=8\text{cm}\). Die Strecke \(DF\) aus dem Tangens
$$ \tan{16,2°}=\frac{DF}{AD} \quad \Rightarrow DF=DA \cdot \tan{16,2°} \approx 1,598\text{cm}$$
Damit kann man dann \(CE\) berechnen (Die Winkel FAD und EFC sind beide =\(16,2°\))
$$\tan {16,2°}=\frac{CE}{DC-DF} \quad \Rightarrow CE=(DC-DF) \tan {16,2°} \approx 1,860 \text{cm}$$
und \(AE\) liefert der Pythagoras
$$AE = \sqrt{AB^2 + (BC-CE)^2}\approx 8,789 \text{cm}$$
Gruß Werner