Der zur y Achse symmetrisch liegende Graph einer Polynomfunktion 4 .Grades
f(x) = a·x^4 + b·x^2 + c
hat im Punkt P (√3 / -4 ) eine waagrechte Tangente
f(√3) = -4
9·a + 3·b + c = -4
f'(√3) = 0
12·√3·a + 2·√3·b = 0
und schneidet die x- Achse im Punkt N ( -1 /0)
f(-1) = 0
a + b + c = 0
Wir erhalten also das LGS
9·a + 3·b + c = -4
12·√3·a + 2·√3·b = 0
a + b + c = 0
Eine Lösung mit dem Additionsverfahren ergibt: a = 1 ∧ b = -6 ∧ c = 5
Unsere Funktion lautet daher:
f(x) = x^4 - 6·x^2 + 5
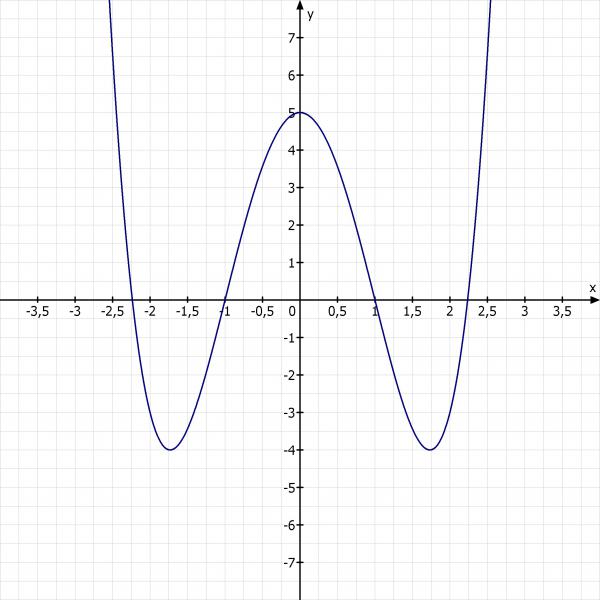
Skizze