1-cos (pi*x) - Nullstellen berechnen

Question

Ich habe diese Frage gestern stellen wollen, und hatte blöderweise einen Fehler gemacht. Daher nochmal ein neuer Beitrag, denn die Nullstellen vom cosinus alleine sind mir klar. :)

Neuer Ausdruck:  1-cos (pi*x)

Answer 1

forme den Ausdruck um zu: $$1-\cos(\pi x)=0\quad\Leftrightarrow\quad\cos(\pi x)=1$$

Wenn Dir die Nullstellen der Cosinusfunktion klar sind, ist Dir sicher auch klar, unter welcher Bedingung der Cosinus =1 ist, oder?

Comments

Ja, cos (xpi)=1 führt zu x=0. Aber abgesehen von dieser Nullstelle finde ich keine anderen mehr, bzw. Ich weiß nicht wie ich auf weitere komme. Das ist mein Problem. Entschuldigung, ich hatte ausführlicher erklären sollen, was mein Problem ist

---

Denk dran, dass der Cosinus $$2\pi$$-periodisch ist ;)

---

Daran habe ich auch gedacht! :D Aber ändert sich die Periode durch das pi nicht  (cos (x*pi)? Und wenn ich mit dieser Periode rechnen würde, also zu 0 immer 2pi dazu rechne, lasse ich da nicht ein paar Nullstellen aus? Sorry für die vielen Fragen, aber das ist das Horrorthema für mich.:(

---

der Cosinus wird =1 für $$2\pi n$$ mit $$n\in\mathbb{Z}$$

Wenn jetzt im Argument schon $$\pi x$$ steht, folgt daraus für x: $$2\pi n=\pi x\quad\Rightarrow\quad x=2n$$

Damit hast Du alle Lösungen der Gleichung.

---

Oh. Okay. Das macht Sinn. Das läuft ja dann auf diese Formel hinaus: 2pi/b.

Answer 2

Aber ändert sich die Periode(nlänge) durch das pi
nicht  cos (x*pi) ?

Ja.

Jetzt nur grundsätzliche Überlegungen zur
Periodenlänge von cos (x*pi)
Hochpunkte
1.
cos ( 0 )  = 1 = cos ( x * pi )
x * pi = 0
x = 0

2.
cos ( 2 * pi ) = 1 = cos ( x * pi )
2 * pi = x * pi
x = 2

3. x = 4 usw

Periodenlänge = 2

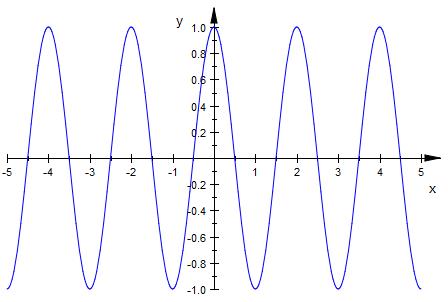
Hochpunkte
x = 0, 2, -2, 4, -4,...

x = y * 2  | y ∈ ℤ

mfg Georg