Hi,
einige Korrekturen zu meiner Lösung
1.
Durch Integration folgt
$$ \frac{1}{2} \ln \left| \frac{y+1}{y-1} \right| = x + \ln(C) $$ und aus der Anfangsbedingung folgt \( C = 1 \) also
$$ \left| \frac{y+1}{y-1} \right| = e^{2x} $$
2.
Damit ergeben sich zwei Lösungen, jenachdem ob \( \frac{y+1}{y-1} >0 \) oder \( \frac{y+1}{y-1} < 0 \) gilt
Einmal ergibt sich
$$ (1) \quad y(x) = \frac{ e^{2x} + 1 }{ e^{2x} - 1 } $$ bzw.
$$ (2) \quad y(x) = \frac{ e^{2x} - 1 }{ e^{2x} + 1 } $$
Nur die zweite Lösung erfüllt die Anfangsbedingung.
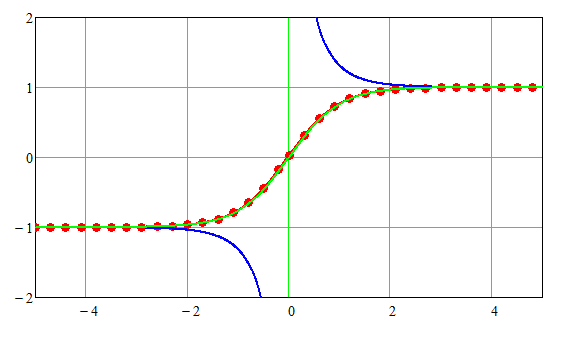
Die blaue Kurve stellt Lösung 1 dar, die grüne Kurve stellt Lösung 2 dar. Die gepunkte Lösung ist numerisch berechnet.