Parabel. Den Faktor a bestimmen , wie?

Question

Ich habe einige Fragen zu den Aufgaben hier :

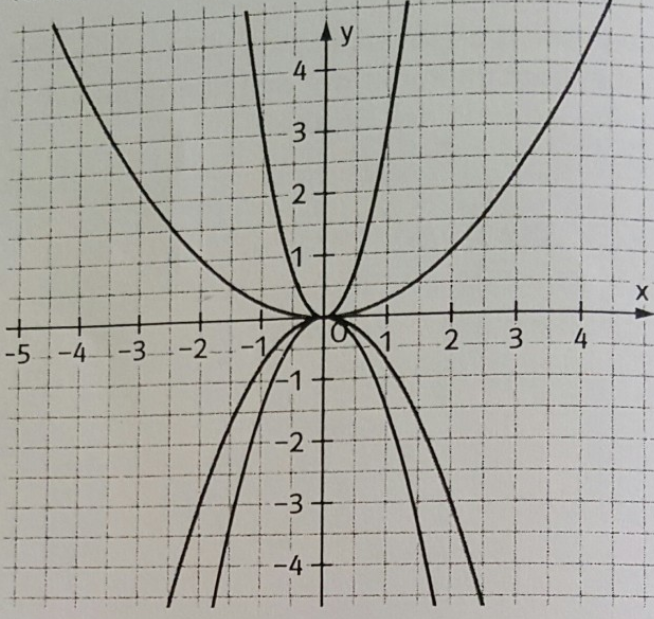
4 Die Graphen gehören zu Funktionen der Form f(x) = ax². Bestimme a. Wähle dazu einen Punkt auf dem Graphen mit gut ablesbaren Werten und setze seine Koordinaten in die Gleichung ein.

5 Die Graphen gehören zu Funktionen der Form \( f(x)=a \cdot\left(x-x_{S}\right)^{2}+  \mathrm{y}_{\mathrm{S}} . \)

Bestimme \( \mathrm{a}, \mathrm{x}_{\mathrm{S}} \) und \( \mathrm{y}_{\mathrm{S}} . \) Beschreibe, wie du vorgehst. Tausche die Beschreibung zu einem Beispiel mit deinem Nachbarn aus.

 Wie kann ich den Faktor a bestimmen bzw. ablesen ? Bei Nummer 5 hängt irgendwie davon zusammen. Könntet ihr bitte helfen . Es würde mir eine große Freude bereiten.

Answer 1

In diesem Bild sind alle a ablesbar:

Das klappt nur exakt, wenn die Scheitelpunkte und die andern Punkte alle exakt auf den Graphen liegen.

D.h. das a=1/2 bei T ist vielleicht nicht genau. Du kannst es genau berechnen mit dem Punkt T.

a* 1.5^2 = 0.9

a = 0.9 / (1.5)^2 = 0.4 

Answer 2

Zu 4) Die schmale nach oben geöffnete Parabel geht durch (1;3). Einsetzen in f(x)=ax² ergibt 3=a·1² oder a=3.

Die breite nach oben geöffnete Parabel geht durch (2;1). Einsetzen in f(x)=ax² ergibt 1=a·2² oder a=1/4

Die schmale nach unten geöffnete Parabel geht durch (1; - 1,5). Einsetzen in f(x)=ax² ergibt -1,5=a·1² oder a= -1,5.

Die breite nach unten geöffnete Parabel geht durch (2; - 3). Einsetzen in f(x)=ax² ergibt -3=a·2² oder a= -3/4.

Answer 3

4.) dürfte geklärt sein

zu 5.)
für die obere rechte Parabel gilt
f ( x ) = a * ( x - xs )^2 + ys
S ( 1 | 1 )
f ( x ) = a * ( x - 1 )^2 + 1
P ( 2 | 4 )
f ( 2 ) = a * ( 2 - 1 )^2 + 1 = 4
a * ( 2 - 1 )^2 + 1 = 4
a * 1 + 1 = 4
a = 3

mfg Georg