Hallo Niki,
zu 18) anbei das Schrägbild.
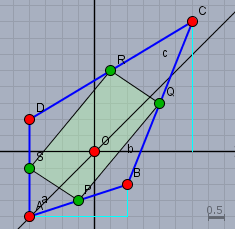
Wenn Dir nicht klar ist, wie das zustande kommt, so frage bitte nach. Ich habe es Dir noch mal als Szene im Geoknecht 3D eingegeben. Drücke auf den Link und bewege das Bild mit gedrückter Maustaste. Dann bekommst Du einen 3-dimensionalen Eindruck der Szene.
Den Mittelpunkt einer Seite berechnet man, indem man die Ortsvektoren zu den Eckpunkten der Seite addiert und das Ergebnis halbiert - das ist das arithmetische Mittel. So kommt man z.B. zum Punkt \(P\)
$$\vec{P} = \frac{1}{2} \left( \vec{A} + \vec{B}\right) = \frac{1}{2} \left( \begin{pmatrix}4 \\ 0\\0 \end{pmatrix}+ \begin{pmatrix}4 \\ 3\\1 \end{pmatrix} \right)= \frac{1}{2}\begin{pmatrix}8 \\ 3\\1 \end{pmatrix}=\begin{pmatrix}4 \\ 1,5\\0,5 \end{pmatrix}$$
Die weiteren drei Mittelpunkte \(Q\), \(R\) und \(S\) werden genauso berechnet. Es ist
$$\vec{Q}= \begin{pmatrix} 2\\ 3\\ 2,5 \end{pmatrix} \quad \vec{R}= \begin{pmatrix} 2\\1,5 \\ 3,5 \end{pmatrix} \quad \vec{S}= \begin{pmatrix} 4 \\ 0 \\ 1,5 \end{pmatrix}$$
Zur Überprüfung, ob es sich bei PQRS um ein Parallelogramm handelt, bestimme ich die Vektoren der Seiten. Es ist
$$\vec{PQ} = \vec{Q} - \vec{P} = \begin{pmatrix} 2\\ 3\\ 2,5 \end{pmatrix}-\begin{pmatrix}4 \\ 1,5\\0,5 \end{pmatrix}=\begin{pmatrix}-2 \\ 1,5\\2 \end{pmatrix}$$ und
$$\vec{SR} = \vec{R} - \vec{S} = \begin{pmatrix} 2\\1,5 \\ 3,5 \end{pmatrix} -\begin{pmatrix} 4 \\ 0 \\ 1,5 \end{pmatrix}=\begin{pmatrix}-2 \\ 1,5\\2 \end{pmatrix}$$
d.h.: \(\vec{PQ}=\vec{SR}\). Da beide Vektoren identisch sind, muss es sich bei PQRS um ein Parallelogramm handeln. Prüfe das selber noch einmal für \(\vec{PS}=\vec{S}-\vec{P}\) und \(\vec{QR}=\vec{R}-\vec{Q}\) selber nach.
Gruß Werner