Lineare Abbildung mit der Spiegelung an der Ebene E.

Question

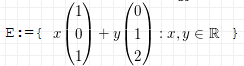
diese Frage hat jemand hier im Forum gestellt, wobei ich den aufgabenteil a) nicht verstanden habe.Wir betrachten in ℝ³ den Untervektorraum:#geometrisch ist dies eine ebene durch den Ursprung. Weiter sei φ:ℝ^{3 →} ℝ ³ die lineare Abbildung, die durch die Spiegelung an der Ebene E gegeben ist.#a) Wählen sie eine Basis B' des , für die die Bilder der Basisvektoren unter φ leicht anzugeben sind, und geben sie die Bilder der Basisvektoren an.Kann mir jemand erklären wie ich die a) lösen kann und insbesondere auf die Spiegelung und in welcher Form dieser für den Aufgabenteil a) relevant ist?

Answer 1

Als Basisvektoren wählst du am besten erst mal die beiden Spannvektoren der

Ebene, die bleiben ja bei der Spiegelung unverändert, sind also je gleich ihrem Bild.

Dann als dritten einen Normalenvektor von E , etwa

( -1  ;   -2   ;  1 ), der hat dann als Bild

( 1  ;   2   ;    -1 ).