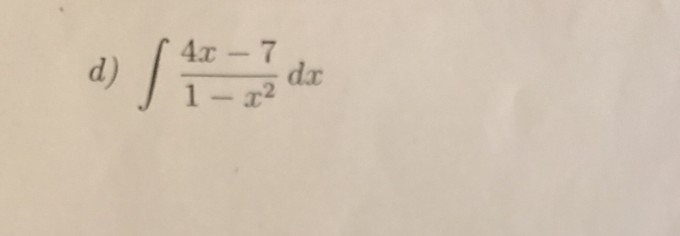integral zur substitution typ 3

Question

folgende Aufgabe soll integriert werden:

(4x-7)/(1-x^2) dx

Zuerstmal hab ich gelernt das bei Typ 3 im Zähler die Ableitung des Nenners stehen soll, was ich hier aber nicht erkennen kann!

Zum zweiten bekomme ich als Lösung immer

 ln(1-x^2)-7 + C heraus.

Der Musterlösung nach wäre die richtige Lösung jedoch:

-2 ln(1-x^2) - 7 artanh(x) + C

Wäre klasse wenn mir jemand  erklären könnte wie das bei der Aufgabe funktionieren soll.

mfg

Comments

Ich persönlich hätte mittels Partialbruchzerlegung integriert.

y = (4·x - 7)/(1 - x^2) = 1.5/(x - 1) - 5.5/(x + 1)

Y = 1.5·LN(|x - 1|) - 5.5·LN(|x + 1|) + C

Answer 1

Meine Berechnung:

Answer 2

Schreibe dir den Term um, sodass du die Ableitung des Nenners im Zähler stehen hast.

y = (4·x - 7)/(1 - x^2) = -2·(-2·x)/(1 - x^2) - 7/(1 - x^2)

Jetzt solltest du es hin bekommen.

Y = -2·LN(1 - x^2) - 7·ATANH(x) + C