Der Kreis des Apollonius ist der Ort aller Punkte, deren Entfernung zu zwei anderen Punkten immer im selben Verhältnis zueinander stehen. In Deinem Fall sind die beiden anderen Punkte die Punkte \(C\) und \(H_c\) des Dreiecks, wenn \(H_c\) der Höhenfußpunkt auf der Seite \(c\) ist. D.h. auch, wenn Du den Kreis des Apollonius zeichnest, deren Punkte alle im Verhältnis 10:3 von \(C\) und \(H_c\) entfernt sind, so schneidet dieser Kreis die Senkrechte zur Höhe \(h_c\) durch den Punkt \(H_c\) in \(A\) und \(B\). Ein Bild dazu:
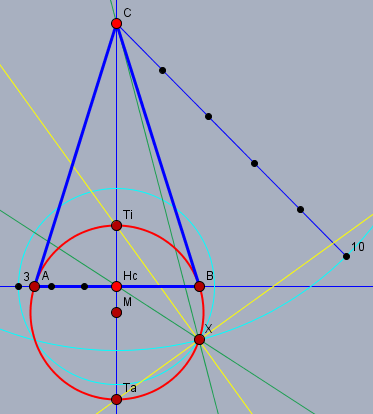
Der rote Kreis ist der Kreis des Apollonius. Die Konstruktion geht wie folgt: Beginne mit der Höhe \(h_C\) mit den Endpunkten \(C\) und \(H_c\). Zeichen um die Punkte \(C\) und \(H_c\) je einen Kreis mit zwei Radien, die im Verhältnis 10:3 lang sind - z.B. 4cm und 1,2cm (hellblau). Diese schneiden sich in einem Punkt \(X\). Verbinde nun \(X\) mit \(C\) und \(H_c\) - das sind die grünen Geraden. Dann konstruiere die Winkelhalbierende im Winkel \(CXH_c\) und die Senkrechte zur Winkelhalbierenden durch \(X\) - die gelben Geraden. Diese schneiden die Verlängerung von \(h_C\) in \(T_i\) und \(T_a\). Der Mittelpunkt dieser beiden Punkte ist der Mittelpunkt des Keises des Apollonius, der durch die Punkte \(T_a\), \(T_i\) und \(X\) verläuft. Er schneidet die Senkrechte durch \(H_c\) in \(A\) und \(B\).
Gruß Werner