Question

Gegeben ist die Funktion f(x)=x 2·exp(-0.5x+2).
Führen Sie eine Kurvendiskussion durch und kreuzen Sie alle richtigen Aussagen an.

a. Im Punkt x=1.80 ist die zweite Ableitung von f(x) negativb. Im Punkt x=4.21 ist die erste Ableitung von f(x) gleich -2.23c. Im Punkt x=4.41 ist f(x) konkavd. Im Punkt x=5.32 ist f(x) steigende. Der Punkt x=0.00 ist ein lokales Maximum von f(x)

Comments

 f(x)=x 2·exp(-0.5x+2) . Sicher? Das ist eine ungewöhnliche Darstellung einer Funktionsgleichung!

Meinst du 

f(x)=x^2·exp(-0.5x+2) oder  f(x)= 2x·exp(-0.5x+2)?

Answer 1

Hallo Jana (?),

f(x) = x² · e^-0,5x+2 

mit der Produktregel erhält man:

f '(x)  =  x * e^-0,5x+2 * (2 - 0,5 x)

f "(x)  =  e^-0,5x+2 * (0,25 x² -2x + 2)

Nullstelle:  x=0

Grenzwerte:  lim_x→∞ f(x) = 0  weil die e-Funktion (→0)  das Polynom überwiegt

                            lim_x→-∞ f(x) =  ∞ 

Extremwerte:  

f '(x) = 0  ⇔  x=0   mit Vorzeichenwechsel - → +   → lokales Minimum T(0|0)  

oder   2 - 0,5x = 0  ⇔ x = 4   mit Vorzeichenwechsel + → -   → lokales Maximum H(416)   

Wendepunkte:  f "(x) = 0  ⇔  0,25 x² -2x + 2 = 0  ⇔  x² - 8x + 8 = 0

    pq-Formel  →   x₁ = 4 - 2·√2  ;  x₂ = 2·√2 + 4  [ y-Werte durch Einsetzen in f(x) ]  

                                                                  

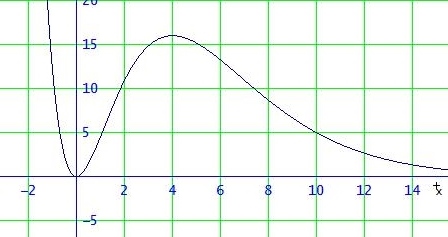
Die Antworten kann man zum Teil im Graph ablesen.

a)  f "(1,8)  ≈  - 2,37  ist negativ 

b)  f '(4,21)  ≈ - 0.398  ≠ -2,23

c)  f "(4,41) ≈ -1.595 < 0  → konkav

d)  f '(5,32) ≈ -1.815  < 0  →  fallend

e)  f '(0) = 0  und  f "(0) = 2e² > 0  →  lokale Minimalstelle  x=0

Gruß Wolfgang

              

Comments

Können Sie mir bitte helfen?

---

Eine eigene Frage mit ein paar eigenen Ansätzen zu der Aufgabe fände ich schon anständig oder?

---

@Mathemathe : bitte stelle deine Frage auch als Frage ein, das erhöht auch die Wahrscheinlichkeit, dass du Hilfe bekommst.

https://www.mathelounge.de/ask

---

Ich kann nicht die Frage als Frage einstellen . Es gibt eigene Probleme deswegen schreibe ich hier :(

---

"Ich kann nicht die Frage als Frage einstellen . Es gibt eigene Probleme deswegen schreibe ich hier :("

Und warum nicht?

---

Keine Ahnung ich hab vielmals probiert.

---

Gab es denn eine Fehlermeldung?