@fragesteller
Wieso dividiert man durch (x-5)?
Die Fkt. hat doch keine Nullstelle bei x=5 oder
wie ist das zu verstehen?
Ich weiß zwar nicht ob ich mittlerweile
langweile aber mir selbst ging die Frage
immer noch durch den Kopf z.B. eine
möglichst anschauliche Antwort auf dieselbe
zu finden.
Skizze 1 zeigt eine beliebige Funktion für die
gesucht wird f ( x ) = 8
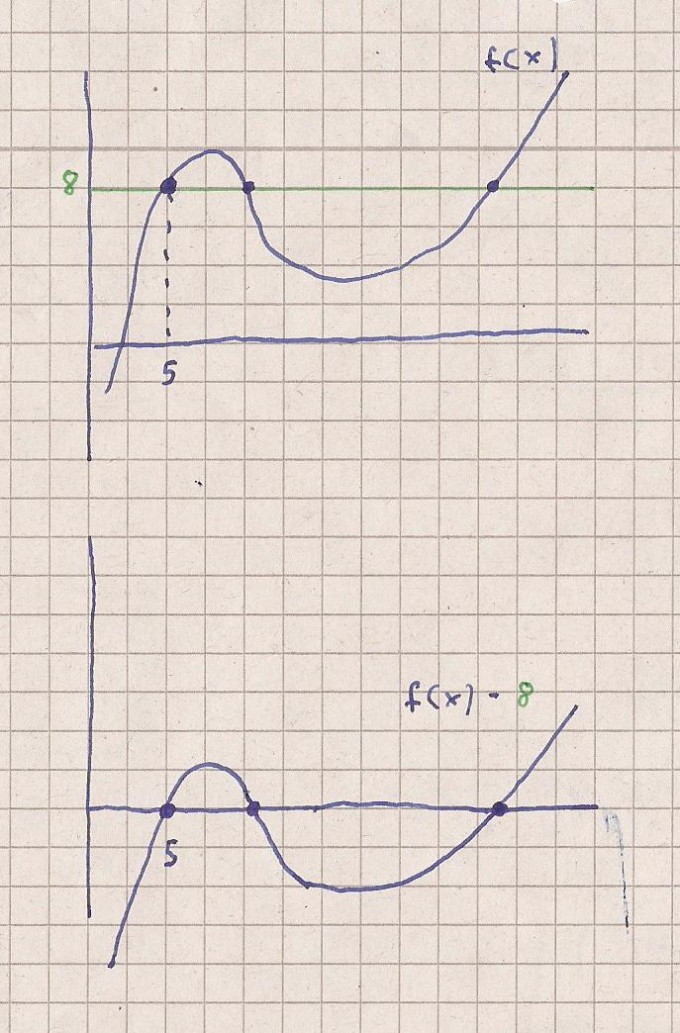
Die Funktion wird nunmehr nach unten verschoben zu
f ( x ) - 8
Die Nullstellen von f ( x ) -8 entsprechen den Stellen
bei f ( x ) = 8