Question

Berechne die Seitenlänge der Dreiecke

Comments

Ich weiß nicht wie ich die einzelnen Seiten berechnen soll 

Answer 1

Hallo Gasti,

Ich habe die Skizze noch mal erweitert:

 

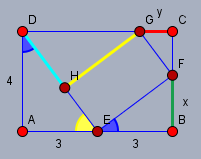
Das Rechteck \(EFGH\) hat in jeder Ecke einen rechten Winkel - also 90°. Also muss die Summe des gelben und blauen Winkels im Punkt \(E\) auch 90° ergeben. Das gilt aber genauso für die Summe des blauen Winkels im Punkt \(D\) und des gelben Winkels im Punkt \(E\), da \(AED\) ein rechtwinkliges Dreieck ist. Daraus folgt, dass die beiden blauen Winkel gleich groß sind.

Folglich ist das Dreieck \(EBF\) ähnlich zum Dreieck \(AED\), da beide rechtwinklig sind und in einem weiteren Winkel überein stimmen.

Mit der gleichen Argumentation kann man jetzt mit den Dreiecken \(FCG\) und \(GDH\) weiter machen. Alle Dreiecke sind ähnlich. Mit dieser Information kann man nun die Seitenlängen berechnen. Auf Grund der Ähnlichkeit muss gelten:

$$\frac{3}{4}=\frac{x}{3} \quad \Rightarrow x=\frac{9}{4}=2,25$$

Und da \(DE=\sqrt{4^2+3^2}=5\) ist, gilt weiter

$$\frac{DE}{4}=\frac{5}{4}=\frac{EF}{3} \quad \Rightarrow EF=\frac{15}{4}=3,75$$

Mit dem Dreieck \(FCG\) geht es genau so weiter. \(FC=4-x\)

$$\frac{3}{4}=\frac{y}{FC}=\frac{y}{4-\frac{9}{4}}=\frac{y}{\frac{7}{4}} \quad \Rightarrow y=\frac{21}{16}\approx 1,31$$

$$\frac{5}{4}=\frac{GF}{4-x}=\frac{GF}{\frac{7}{4}} \quad \Rightarrow GF=\frac{35}{16} \approx 2,19$$

und beim Dreieck \(GDH\) startet man mit der Seite \(HG\), die ja genauso lang ist wie \(EF\) (s.o.) Das schaffst Du jetzt bestimmt alleine.

Comments

da AED ein rechtwinkliges Dreieck ist.

Warum sind dann im inneren Viereck vier (!) rechte Winkel markiert im äußeren Viereck aber nicht ein einziger ?

---

Du fragst: "Warum sind dann im inneren Viereck vier (!) rechte Winkel markiert aber im äußeren Viereck aber nicht ein einziger ?"

Das wird wohl die künstlerische Freiheit des Autors dieser Aufgabe sein. Das Viereck ABCD ist IMHO ein Rechteck. Falls es das nicht wäre, wäre die Aufgabe auch nicht eindeutig lösbar.

---

Hallo vk314,

Das Verhältnis zu Dreieck IV kann ich nicht bestimmen.

... ohne Pythagoras geht es auch:

Wenn Du die Strecke  \(|BF|=2,25\text{cm}\) hast, ist \(|CF|= (4-2,25)\text{cm} = 1,75\text{cm}\). Die Strecke \(|CG|\) ist \(|CG| = \frac34 |CF| = \frac{21}{16} \text{cm}\). (hast Du - Ok!)

Die Maße des Rechtecks \(EFGH\) kann man auch über die Flächenbetrachtung bestimmen.

Die Kongruenz von \(\triangle EBF\) und \(\triangle GKH\) lässt sich wie oben zeigen und da \(|EF|=|GH|\) sind, sind beide Dreiecke auch identisch. Daraus folgt die Höhe \(|HK|=|BF|\) in \(\triangle GDH\)  Damit lässt sich die Fläche \(F_D\) aller 4 Dreiecke berechnen:
$$F_D = \frac12 \left( 3\cdot 4 + 3 \cdot \frac94 + \frac{21}{16} \cdot \frac{7}{4} + \frac{75}{16} \cdot \frac94 \right)\text{cm}^2 = \frac{1011}{64} \text{cm}^2$$ Das Seitenverhältnis des Rechtecks muss sein:

$$\frac{|EH|}{|EF|} = \frac{|CF|}{|EB|} = \frac{7}{4 \cdot 3} = \frac{7}{12}$$ Daraus folgt dann z.B. die Seite \(|EF|\)

$$|EF| = \sqrt{ \frac{12}{7} \left(24 \text{cm}^2 - \frac{1011}{64} \text{cm}^2\right)} = \frac{15}{4}\text{cm} = 3,75 \text{cm} \\ |DE| = \frac43 |EF| = 5\text{cm}$$ usw.

---

Ok super, danke! Das wird zum jetzigen Zeitpunkt aber zu viel sein. Hätte mir gewünscht, dass es eine Lösung innerhalb des Themas gibt. Also ohne Flächen. LG und danke nochmal

---

Also ohne Flächen.

Du bist ganz schön anspruchsvoll ;-)

Aber bitte: Vergleiche \(\triangle GDH\) und \(\triangle FEB\). Es ist

$$\frac{|HG|}{|DG|} = \frac{|EB|}{|EF| = |HG|} \\ \space \Rightarrow |EF|=|HG| = \sqrt{|EB|\cdot|DG|} = \sqrt{\frac{3 \cdot 75}{16}} \text{cm} = 3,75\text{cm}$$

Zugegebender Maßen ist das auch noch einfacher. Man muss eben drauf kommen. Das größte Hindernis für eine elegante Lösung ist die Existenz einer anderen.

---

Also ohne Flächen

Δ_1 ~ Δ_2  ⇒  4/3 = 3/a  ⇒  a = 9/4

b = 4-a = 7/4

Δ_2 ~ Δ_3  ⇒  3/b = a/c  ⇒  c = a·b/3  =  21/16

d = 6-c = 75/16

Δ_2 ~ Δ_4  ⇒  3/y = y/d  ⇒  y^2 = 3d = 225/16  ⇒  y = 15/4

Δ_4 ~ Δ_1  ⇒  y/x = 4/3  ⇒  x = 3y/4 = 45/16

Δ_2 ~ Δ_3  ⇒  3/b = y/z  ⇒  z = b·y/3 = 35/16

(Kontrolle für Fans Pythagoräischer Tripel : x+z = 5)

---

Ah genau, das ist es, danke! Jetzt wird sie doch gemacht, denn Verhältnisse sind innerthematisch.

Tolles Forum!

LG

Answer 2

Die Katheten von I sind gegeben. Ihr Verhältnis ist: längere Kathete/kürzere Kathete =4/3. Dieses Seitenverhältnis muss für alle Dreiecke gelten. Dann hat II die Kathetenlängen 3 und 9/4. Die längere Kathete von III berechnet sich dann als 4 - 9/4 =7/4. Wenn wir dei kürzere Kathete jetzt x nennen, muss gelten (7/4)/x=4/3. daher ist x=21/16. Dann ist die Hypotenuse von IV 6 - 21/16=75/16.

jetzt brauchst du die Katheten von iV und die Hypotenusen von I, II und III. Dazu nur so viel: Die Hypotenuse von I ist 5 (Pythagoas). Wenn du nicht weiter kommst, melde dich nochmal.

Comments

ist zwar eine Weile her, aber die Schüler haben zu dem Zeitpunkt noch keinen Pythagoras. Wie kommt man auf die 5 cm bei DE, wenn man Pythagoras nicht kennt?

Das Verhältnis zu Dreieck IV kann ich nicht bestimmen. 

---

Bist du sowohl vk314 als auch Gasti?

Woher weißt du, dass Gasti den Pythaqgoras noch nicht kennt?

"Das Verhältnis zu Dreieck IV kann ich nicht bestimmen."

Darf ich annehmen, dass du das Seitenverhätnis in III bestimmen kannst?

---

Ja, sorry, habs zwei mal abgeschickt. Bin Lehrer und hab die Aufgabe nächste Stunde vor. Ist das erste Kapitel im Buch, Pythagoras kommt erst später. Daher muss es ohne gehen, oder es iat ein Fehler im Buch.

LG

---

Dreiecke I-III sind mit Verhältnissen ihrer Katheten bekannt, nicht jedoch die Hypotenusen.

---

Wie kommt man auf die 5 cm bei DE, wenn man Pythagoras nicht kennt?

ich habe unter meiner Antwort noch eine Lösung hinzugefügt, die ohne den Satz des Pythagoras auskomt.

---

Zunächst mal finde ich gut,dass du in diesem Forum nach Aufgaben für deinen Unterricht suchst. Was du allerdings selbst nicht heraus bekommst, eignet sich meistens auch nicht für den Unterricht. Obwohl man da Überraschungen erleben kann. Ich persönlich fürchte,dass man die Hypotenusen ohne Pythagoras nicht bestimmen kann - außer man kennt das 3,4,5-Dreieck.

---

Obwohl man da Überraschungen erleben kann.

Der Vorteil der Schüler liegt darin, dass sie noch nicht so viel wissen.Und dann kommen sie eher auf Lösungen, die nur aus den Bausteinen bestehen, die sie schon gelernt haben (z.B. Fläche von Drei- und Viereck)!

Unsere 'Standardlösungen', die Du und ich sehen, wirken ab und an wie Scheuklappen!

---

@ Werner-Salomon. Ja, das mit den Scheuklappen ist wahr. Über Flächenberechnungen geht es vermutlich.

---

Über Flächenberechnungen geht es vermutlich.

nicht nur 'vermutlich'. Siehe meinen Kommentar hinter meiner Antwort.