Geradengleichung & Normalparabel

Question

Wie lautet die Gleichung der Geraden durch den Punkt (0/2), welche die Normalparabel in S (3/?) schneidet? Geben Sie auch den zweiten Schnittpunkt an.

Wie löst man so etwas?

Answer 1

Hallo ib,

> Wie lautet die Gleichung der  Geraden  durch den Punkt (0/2), welche die Normalparabel in S (3/?) schneidet? Geben Sie auch den zweiten Schnittpunkt an.

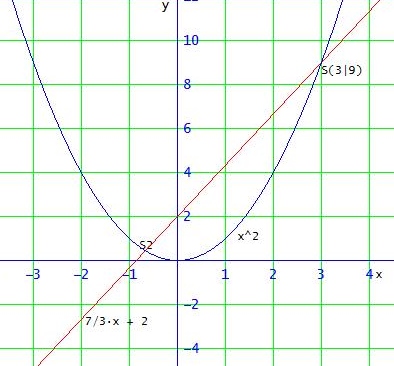
Der Punkt S liegt auf der Parabel  y = x² und hat deshalb die y-Koordinate  y = 3² = 9 

→  S(3|9)

Deshalb hat die Gerade y = mx + b durch  P und S die Steigung m = (9 - 2) / (3 - 0) = 7/3

b ist der y-Achsenabschnitt der Geraden, wegen P(0|2)  →  b = 2

→  y = 7/3 · x + 2 

Den 2. Schnittpunkt mit der Normalparabel findet man durch Gleichsetzen:

x² =  7/3 · x + 2 

x² - 7/3 · x - 2 = 0

pq-Formel →    x₁ = - 2/3   ;  x₂  = 3

(-2/3)² = 4/9   →   S₂ (-2/3 | 4/9)

Gruß Wolfgang