Aufgaben mit Geradengleichung etc

Question

Aufgabe:

Der aus dem Stück einer Geraden g und einer Parabel f knickfrei zusammengesetzte Graph beschreibt den Querschnitt eines 30m hohen Damms. Die Steigung von g ist 0,8, die Parabel ist der Graph von f mit \(f(x)=-\frac{1}{20}x^2+20\).

A) Berechnen Sie die Geradengleichung und die Länge des Querschnitts CD.

B) Auf dem Damm steht ein 2m hoher Stab. Prüfen Sie, ob man vom Punkt P(25|0) die Spitze des Stabes sehen kann.

Problem/Ansatz:

Hallo ich benötige Hilfe bei der Hausaufgabe und eine Erklärung ebenfalls.

Comments

Da von der

Länge des Querschnitts CD

die Rede ist, solltest Du klarstellen, was C und was D ist.

Soll der Damm wirklich 30 m hoch sein?

---

Eine Skizze mit Beschriftung solltest Du schonmal als Start selbst liefern. Dazu dann Deine konkreten Fragen, wo das Problem ist.

---

Da steht bei a) berechnen sie die geradengleichung und die Länge des Querschnitts CD dadrüber ist ein Strich

---

Also der Abstand von C und D . C=Nullstelle von g . D=Nullstelle von f

---

D=Nullstelle von f

f hat zwei Nullstellen. Welche ist gemeint?

---

Ja, C und D werden Punkte auf der Skizze des Damms sein, nur welche?

Ist f(x) korrekt oder muß das …+ 30 (statt 20) heißen?

---

Das steht so f(x)

Text erkannt:

\( f(x)=-\frac{1}{20} x^{2}+20 \)

---

Das paßt nicht zur angegebenen Höhe von 30m.

---

Siehe meine Frage weiter oben: "Soll der Damm wirklich 30 m hoch sein?"

---

Es tut mir leid der damm ist 20m hoch

---

Es tut mir wirklich leid habe mich verschrieben es sind 20m .Und wie und was sollte ich jetzt rechnen ?

---

Wie es aussieht, muss unter anderem bestimmt werden, wo die Parabel die Steigung 0,5 aufweist. Das könntest du ja mal berechnen.

---

wo die Parabel die Steigung 0,5 aufweist.

0,8 ist gefragt.

---

wo die Parabel die Steigung 0,5 aufweist.

0,8 ist gefragt.

Ja, das ist richtig. Ich war wohl noch nicht ganz wach...

Answer 1

A) Du hast einen Punkt (dort wo die Parabel die Steigung 0,8 hat) und die Steigung der Geraden. Verwende die Punkt-Steigungs-Form der Geradengleichung.

B) Du hast zwei Punkte einer geradlinigen Sichtverbindung. Stelle fest, wo sich diese zweite Gerade und die Parabel schneiden. Falls es keine Lösung gibt, besteht eine Sichtverbindung.

Answer 2

Hallo,

1. Ableitung = Steigung

Berechne also, an welcher Stelle (S) f(x) die Steigung 0,8 hat.

Bestimme die Gleichung der Tangente an dieser Stelle und ihre Nullstelle (C).

Berechnet die Nullstelle von f (D), und dann den Abstand zwischen beiden Punkten.

Ein 2 m hoher Stab, der auf der höchsten Stelle des Damm angebracht ist, endet im Punkt Q (0|22).

Stelle die Gleichung der Geraden durch P und Q auf. Wenn sie die Parabel schneidet, ist die Spitze nicht zu sehen.

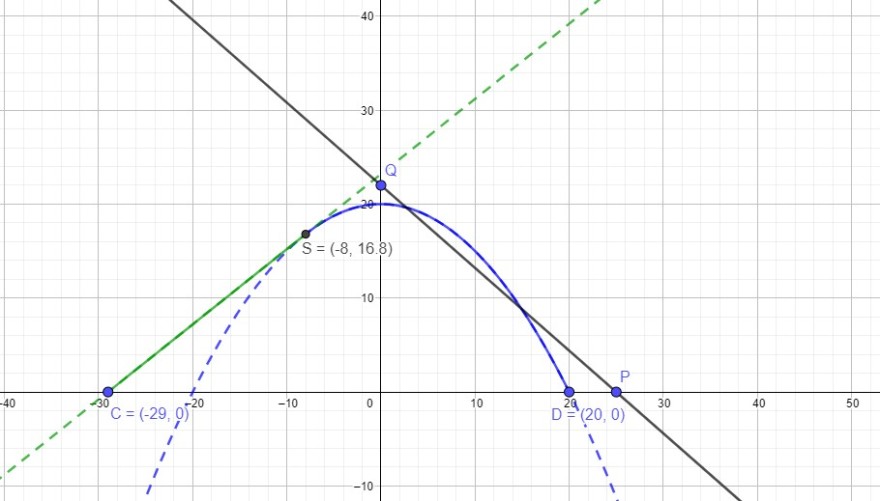
Melde dich, falls du noch Fragen hast.

Gruß, Silvia