Zeichnen Sie den Graphen der Funktion und bestimmen Sie den Differenzenquotienten. f(x)=x^2

Question

Zeichnen sie den Graphen der Funktion f mit f(x) = x² und bestimmen sie den Differenzenqoutienten geometrisch im angegebenen Intervall. Überprüfen sie Ihr Ergebnis rechnerisch

a) I=[0;2]

c) I=[-1;1]



Am liebsten sind mir ganz leicht zu verstehende Antworten

Answer 1

Hi,

Mal die Parabel in ein Koordinatensystem. Bestimme dann die Stellen 0 und 2. Dort trägst Du dann eine Gerade ab, welche durch diese beiden Punkte geht und Du hast Deine Sekante, die sich durch den Differenzenquotienten ergibt. Rechnerisch funktioniert das über:

φ(x₁,x₀) = ( f(x₁)-f(x₀) )/( x₁-x₀ ) = ( x₁² - x₀² )/( x₁-x₀ ) = (4-0)/(2-0) = 2

Überprüfe also, ob Deine Sekante die Steigung 2 hat. Sollte so aussehen:

 

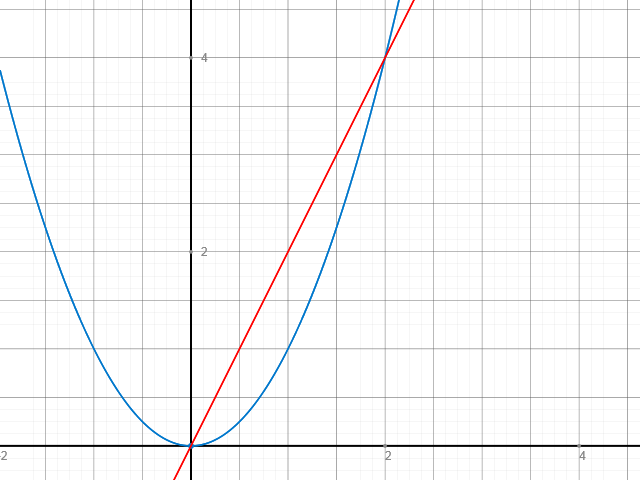
Für das zweite Intervall genau so vorgehen.

Rechnerisch solltest Du auf

φ(x₁,x₀) = ( x₁² - x₀² )/( x₁-x₀ ) = (1-1)/(-1-1) = 0/(-2) = 0

kommen.

Sieht so aus:

 

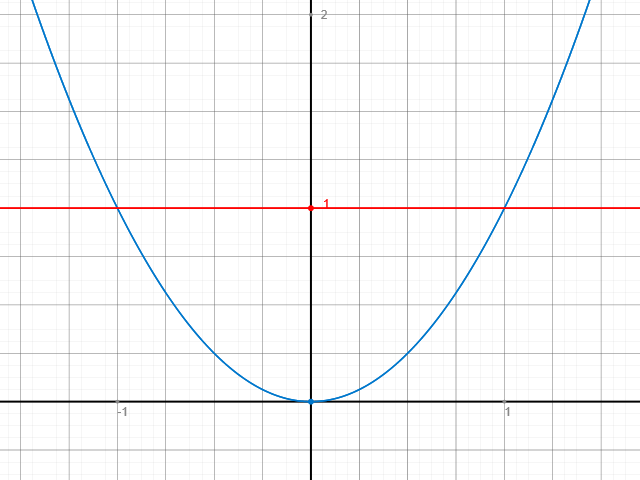
Alles klar?

Grüße